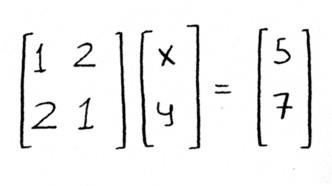Artificial intelligence is trained on data. It will process billions of words of human text, countless images, and the inane, ridiculous questions of its human users. It will learn to write in the active voice most of the time, and to keep sentences under 200 characters. It will learn that dogs have four legs and the Sun is normally yellow. And it might learn that Lorraine Woodward of Ontario wants to know how to prevent the buildup of ear wax.
Most of what we feed into AI has been made by a human — human art, human text, human prompts. And so, it’s clear that AI will inherit the biases and prejudices of human intelligence. For example, a lot has been written about how “racist” and “sexist” AI is.
“Draw a picture of a doctor,” we might prompt.
AI whirrs through its stock catalogue, where 80% of its doctor images are white, male, and gray-haired. It creates the most likely image of a “doctor” the user requires. Is this a kind of racism and sexism? It certainly propagates both, but it’s not really the AI’s fault. It’s ours.
In this week’s Mini Philosophy interview, I spoke with anthropologist Christine Webb about human exceptionalism — “the belief that humans are the most superior or important entity in the Universe” — and how it leaks into our science, ethics, and, increasingly, our AI. Her worry isn’t just about the limits of artificial “intelligence,” but also how damaging it might turn out to be.
The value-free science full of values
A lot of Webb’s work, both in and outside of her book, Arrogant Ape, is directed at calling out “anthropocentrism” in science and technology. Webb has argued that human exceptionalism embedded in mainstream scientific practice has shaped what we study, how we study it, and what we conclude — even when science presents itself as value-free. As she put it in a paper with Kristin Andrews and Jonathan Birch, “values drive research questions, methodological choices, statistical interpretation, and the framing of results,” which means those values can “influence empirical knowledge as much as the data.”
Here are three examples:
Research questions: Animal welfare science often asks how to optimize productivity or “reduce stress” within farming systems, rather than what environments animals themselves would choose. A common study question might be, “What cage enrichment reduces feather-pecking in hens?” rather than, “Do hens prefer to live caged or uncaged at all?” The bias is that the first question assumes or glosses over the legitimacy of caging, tacitly accepting the human agricultural system as the baseline.
Methodological choices: In our interview, Webb pointed out that when comparing cognition between humans and other primates, researchers typically use human-designed tasks (touchscreens, puzzles, symbols). These setups often require fine motor control or familiarity with human artifacts. As a result, apes “underperform,” leading to the conclusion that humans are smarter. But the methods themselves privilege human-like skills. The test is designed for humans to win.
Statistical interpretation: Statistical “significance” thresholds (like p < 0.05) are used to declare that an effect exists or not, but these conventions were originally developed for tightly controlled laboratory and industrial experiments. In animal welfare studies, subtle behavioral changes — like shifts in grooming, gaze, or social spacing — may be dismissed as “not significant,” even though they reflect genuine distress or preference.
AI that looks just like us
When we think about artificial intelligence, we are really talking about artificial human intelligence. Large language models and machine learning technologies are built on human data, operate from human prompts, and give human-like responses.
AI research asks how to make systems useful for humans (more accurate, more personalized, more profitable), not how they might affect nonhuman or ecological systems in terms of energy use, resource extraction, or long-term environmental stability. The framing already presupposes anthropocentrism.
The language we use often betrays both anthropocentrism and anthropomorphism — where we imagine nonhuman things as behaving and thinking just like humans. For example, researchers often describe models as “hallucinating,” “reasoning,” or “aligning” — all metaphors that project human cognition onto statistical systems. The framing centers our self-image rather than the system’s actual operations.
But the most obvious example of anthropocentrism in AI is that the entire field is focused on building intelligence in the same way as humans. It involves neural networks, symbolic reasoning, and goal-directed behavior.
Lessons from a moss
Of course, this makes sense if we want a product that humans can interact with. It makes sense if we want to develop human technology, human medicine, and human progress. But Webb points out that AI research focuses disproportionately on the good of human intelligence while ignoring the problems of “environmental destruction, decay, and arrogance with how we deal with the environment.”
In our conversation, Webb gave an interesting alternative that I’d love to see as a science fiction short story one day. And that’s to imagine an AI with the intelligence of a moss. As Webb put it:
“Robin Wall Kimmerer writes a lot in her work about how mosses have been around for 500 million years or something like that, compared to humans’ meager, like, 200,000 years. And so if we were really interested in intelligence, in living well, and in evolutionary success, maybe we should turn to other forms of life like mosses, who’ve managed to do it for hundreds of millions of years and ask them for solutions to some of the ecological problems that we’re facing today.
And how would we use that intelligence? Well, mosses are amazing, because they survive not by outcompeting others, but by creating highly diverse, thriving environments for other species to survive in. Like, that’s how they survive: by creating these tight, multi-species communities. So that would be a great thing to learn from about.”
We needn’t abandon the entire AI project to see the reasoning in Webb’s argument. If AI is HI but bigger, then it will amplify both the good and the bad. The trade-offs will be on a different scale. And when we’re talking about superhuman-like intelligence, does that mean super destruction, super bugs, and super catastrophe? Because human intelligence does all that. If we’re wanting to build an intelligence that can change the world, should we include a few more members of that world first?
This article The bias that is holding AI back is featured on Big Think.
This post assumes you know algebra, but no linear algebra. Lets dive in.
There are two big ideas I want to introduce in the first chapter: Gaussian elimination, (which is not strictly a linear algebra thing, and has been around for years before linear algebra came along), and row picture versus column picture, which is a linear algebra thing.
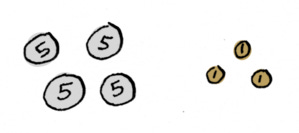
Money example
Let’s say you have a bunch of nickels and pennies, and you want to know how many of each do you need to have 23 cents.
You could write that as an equation that looks like this:
x is the number of nickels you need, y is the number of pennies you need. And you need to figure out the x and y values that would make the left-hand side work out to 23. And this one is pretty easy, you can just work it out yourself. You’d need four nickels and three pennies.
So x is four, y is three.
This kind of equation is called a linear equation. And that’s because when you plot this equation, everything is flat and smooth. There are no curves or holes. There isn’t a ^2 in the equation for example to make it curved. Linear equations are great because they’re much easier to work with than curved equations.
Aside: Another solution for the above is 23 pennies. Or -4 nickels + 43 pennies.
The point is you have two variables (x and y for nickels and pennies), and you are trying to combine them in different ways to hit one number. The trouble starts when you have two variables, and you need to combine them in different ways to hit two different numbers. That’s when Gaussian elimination comes in. In what world would you have to hit two different numbers? Does that seem outlandish? It’s actually very common! Read on for an example.
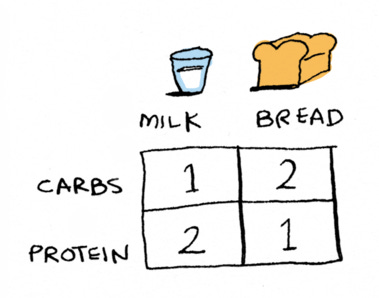
Food example
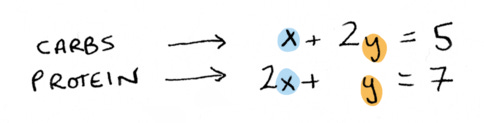
Now let’s look at a different example. In the last one we were trying to make 23 cents with nickels and pennies. Here we have two foods. One is milk, the other is bread. They both have some macros in terms of carbs and protein:
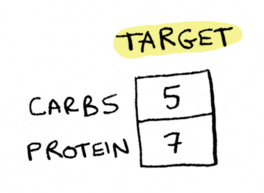
and now we want to figure out how many of each we need to eat to hit this target of 5 carbs and 7 protein.
This is a very similar question to the one we just asked with nickels and pennies, except instead of one equation, we have two equations:
Again we have an x and a y. Lets find their values. To solve these kinds of questions, we usually use Gaussian elimination. If you’ve never used Gaussian elimination, strap in.
Gaussian elimination
Step one is to rewrite this as a set of two equations:
Now you subtract multiples of one equation from another to try to narrow down the value of one variable. Lets double that second equation:
See how we have a +2y and a -2y now? Now we can add the two equations together to eliminate y:
We’re left with one equation and one variable. We can solve for x:
Aha, we know x = 3. Now we can plug that into one of the equations to find y.
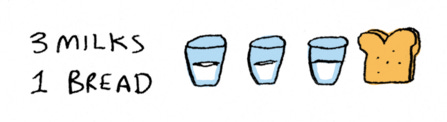
We plug that in to one of the equations and find out that y equals 1, and there we have answer: three milks, one bread, is what we need.
This method is called Gaussian elimination, even though it was not discovered by Gauss. If you haven’t seen Gaussian elimination, congratulations, you learned a big idea! Gaussian elimination is something we will talk about more. It’s part of what makes linear algebra useful.
We can also find the solution by drawing pictures. Let’s see how that works.
Picture version
Let’s plot one of these lines. First, we need to rewrite the equations in terms of x.
Reminder: first equation is for carbs, second for protein. x is number of milks, y is number of breads.
Now let’s plot the graph for the first equation.
Now, what does this line represent?
It’s all the combinations of bread and milk that you can have to get exactly five carbs:
So you can eat no milk and two-and-a-half breads, or two milks and one-and-a-half breads, or five milks and no bread, to get to exactly five carbs. All of those combinations would mean you have eaten exactly five carbs. You can pick any point that sits on this line to get to your goal of eating five carbs.
Note: You can see the line goes into the negative as well. Technically, 5 breads and -5 milks will give you 5 carbs as well, but you can’t drink negative milks. For these examples, let’s assume only positive numbers for the variables.
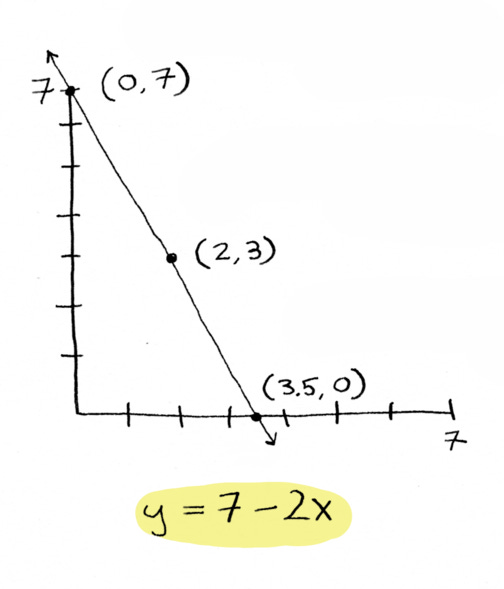
Now, let’s plot the other one. This is the same thing, but for protein.
If you eat any of these combinations, you’ll have met the protein goal:
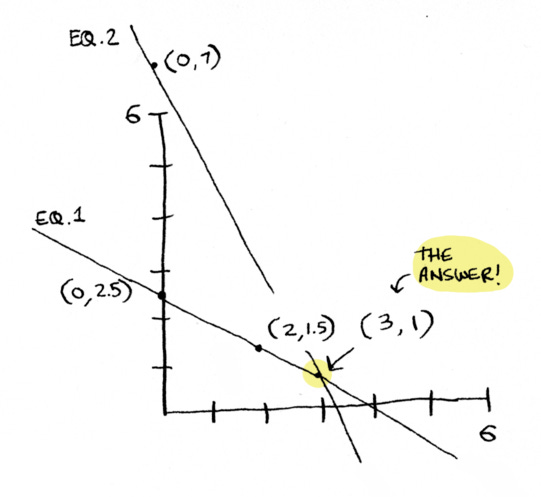
You can pick a point that sits on the first line to meet the carb goal. You can pick a point that sits on the second line to meet the protein goal. But you need a point that sits on both lines to hit both goals.
How would a point sit on both lines? Well, it would be where the lines cross. Since these are straight lines, the lines cross only once, which makes sense because there’s only a single milk and bread combo that would get you to exactly five grams of carbs and seven grams of protein.
Now we plot the lines together, see where they intersect, and that’s our answer:
Bam! We just found the solution using pictures.
So that’s a quick intro to Gaussian elimination. But you don’t need linear algebra to do Gaussian elimination. This is a technique that has been around for 2,000 years. It was discovered in Asia, it was rediscovered in Europe, I think in the 1600s or something, and no one was really talking about “linear algebra”. This trick is just very useful.
That’s the first big idea you learned. You can stop there if you want. You can practice doing this sort of elimination. It’s a very common and useful thing.
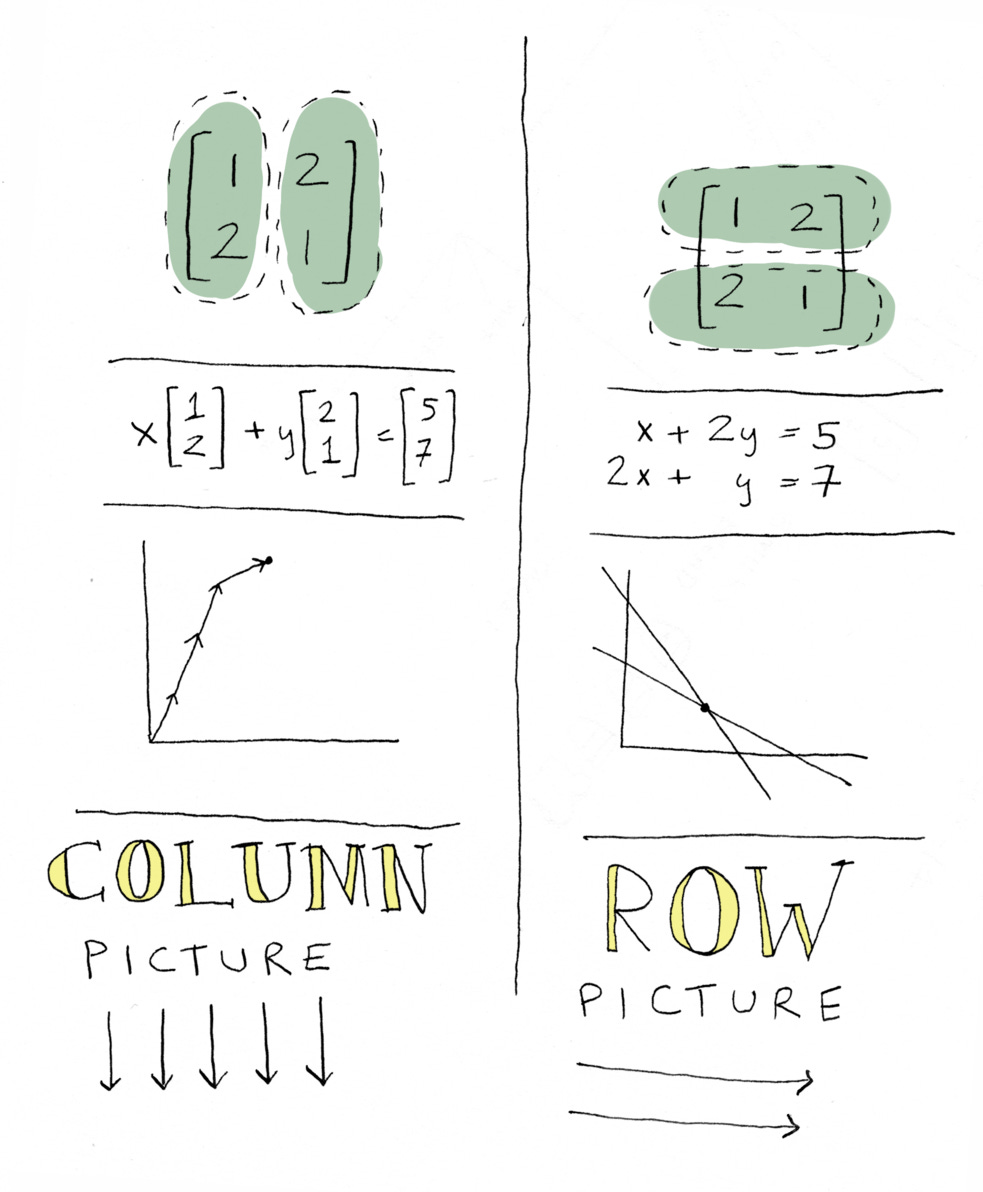
The column picture
What we just saw is called the “row picture”. Now I want to show you the column picture. I’m going to introduce a new idea, which is: instead of writing this series of equations, what if we write just one equation? Remember how we had one equation for the nickels and pennies question?
What if we write one like that for food? Not a system of equations, just a single equation? What do you think that would look like? Something like this:
It’s an equation where the coefficients aren’t numbers, they’re an “array” of numbers. The big idea here is: what if we have a linear equation, but instead of numbers, we have arrays of numbers? What if we treat [1 2], the way we treat a number?
Can that actually work? If so, it is pretty revolutionary. Our whole lives we have been looking at just numbers, and now we’re saying, what if we look at arrays of numbers instead?
Let’s see how it could work in our food example. What if the coefficients are an array of numbers? Well, this way of thinking is actually kind of intuitive. You might find it even more intuitive than the system of equations version.
Each of these coefficients are called vectors. If you’re coming from computer science, you can kind of think of a vector as an array of numbers (i.e. the order matters).
Lets see how we can use vectors to find a solution to the bread and milk question.
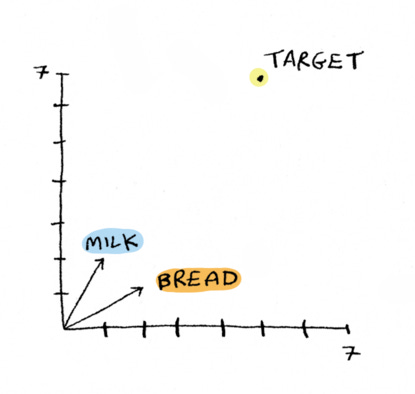
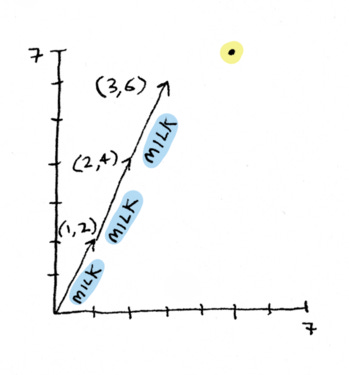
Step one: graph the vectors.
Yeah, we can graph vectors. We can graph them either as a point, like I’ve done for the target vector here, or as an arrow, which is what I’ve done with the vector for bread and the vector for milk:
Use the two numbers in the vector as the x and y coordinates.
That is another big idea here: We always think of a set of coordinates giving a point, but you can think of vectors as an arrow instead of just a point.
Now what we’re asking is how much milk and how much bread do we need, to get to that point?
This is a pretty simple question. It’s simple enough that we can actually see it. Let me add some milks:
And let me add a bread. Bingo bango, we’re at the point:
Yeah, we literally add them on, visually. I personally find this more intuitive. I think the system of equations picture can confuse me sometimes, because the initial question was, “how much bread and how much milk should I eat?” The vector way, you see it in terms of breads and milks. The row way, you see it as one of the lines is the carbs, the other line is the protein, and the x and y axes are the amount of bread, which results in the same thing, but it’s a little more roundabout, a little more abstract. This one is very direct.
The algebra way
We just saw that we can graph vectors too. Graphing it works differently from graphing the rows, but there is a graph we can make, and it works, which is pretty cool. What about the algebra way?
Here is the equation again:
Since we already know the answer, I’ll just plug that in:
Now, the question is how does the left side equal the right side? The first question is how do you define this multiplication? Well, in linear algebra, it’s defined as, if you multiply a scalar by a vector, you just multiply it by each number in that vector:
Now you are left with two vectors. How do you add two vectors? Well, in the linear algebra you just add the individual elements of each vector:
And you end up with the answer.
Congratulations, you’ve just had your first taste of linear algebra. It’s a pretty big step, right? Instead of numbers, we’re working with arrays of numbers. In future chapters, we will see why this is so powerful.
That’s the first big concept of linear algebra: row picture vs column picture.
Finally, I’ll just leave you with this last teaser, which is: how would you write these two equations in matrix notation? Like this:
This is the exact same thing as before. You can write it as scalars times columns, as we had done before:
or you can write it as a matrix times a vector, as above. Either one works.
Matrices are a big part of linear algebra. But before we talk about matrices, we will talk about the dot product, which is coming up next.
Additional reading
Check out Gilbert Strang’s lectures on linear algebra on YouTube.
Summary
Juggling
I can juggle. It’s a fun little skill to pull out from time to time. Most years I try to teach students the basics of juggling at some point, maybe during homeroom or when we have some free time after state testing or something like that. Usually leads to some goofy fun.
Students often think that to learn how to juggle, they should try juggling with three balls right away. They always want to grab three, and start trying to keep them all in the air.
The actual best way to learn to juggle is to start with one ball. Practice throwing from both hands so the ball reaches about the top of your head (experienced jugglers will keep their tosses lower, but head height is good for beginners). After some practice with one ball, move to two balls. Toss one, then toss the other. The goal is for the two tosses to look a bit like the McDonald’s arches: about the same height, offset horizontally. Here it’s important to practice for a while. Get better at that exchange — tossing the second ball while that hand prepares to catch the first ball. Start with both the right hand and the left hand. Make sure the tosses stay the same distance from your body and don’t creep forward. Make sure they’re the same height. Only after a lot of practice with two balls is it time to go to three.
Break It Down
I don’t take teaching juggling too seriously. It’s a fun activity to kill a bit of time with students. But juggling is a good illustration of a broader principle: the best way to learn skill X often isn’t to practice skill X. The best way to learn is often to break skill X into sub-skills A, B, C, and so on, then practice A, B, and C, and work your way up to X.
Here are a bunch of education examples:
To help students get better at word problems, don’t just give students lots of word problems.
To help students get better at taking standardized tests, don’t just give students lots of mock standardized tests.
To help students become better readers, don’t just ask students to read lots of books.
To help students get better at math fact fluency, don’t just give students lots of math fact practice.
To help students write better essays, don’t just ask them to write lots of essays.
To help students write better explanations, don’t just ask them to write lots of explanations.
To help students improve their problem-solving, don’t just give students lots of challenging problems.
To help students get better at note-taking, don’t just ask them to take notes all the time.
To help students get better at collaboration, don’t just assign lots of group projects.
I think every teacher has been guilty of this type of thinking. I know I have.
Juggling isn’t the best example here. I don’t think I’ve met a middle schooler who already knows how to juggle. Students start on a pretty level playing field. But that’s not the case for academic learning. If I’m teaching word problems, some students already have pretty strong word problem skills. Others really struggle. The students who already have strong skills will probably benefit from some broad practice where I throw a bunch of random word problems together and say “practice your word problem skills.” But others will flounder unless that skill is broken down into smaller pieces.
Helpful For All, Harmful For None, Crucial For Some
There’s a nice quote about teaching phonics from Snow & Juel: phonics is “helpful for all children, harmful for none, and crucial for some.” Phonics is just one example of breaking a complex skill down into small pieces. And the tricky thing about this type of teaching is that not all students need it. But for some students it’s absolutely essential. The reasons for that difference are beyond the scope of this post, but the consequences are straightforward. Teaching without breaking learning down into small, manageable steps will work for some students, but not for others. Breaking learning into small steps is the best strategy to help all students make progress. It might be intuitive that, if I want to help students write better explanations for their mathematical thinking, I should ask them to explain their reasoning all the time. It’s also an easy way out: ask for lots of explanations, watch some students write great explanations, pat myself on the back, and call it a day. Much harder is to figure out the component parts of writing a great explanation, teach them one at a time, and help many more students develop a new skill they struggled with before.
The toughest part here is figuring out the components of these skills. They’re not obvious. Unfortunately, that’s how the human mind works: as we become proficient with a skill, the little pieces of that skill melt away and become invisible to us. One of the most important challenges of teaching is finding new ways to break skills down into smaller, more manageable pieces. It never ends. Every year I find new ways to break things down, to figure out which pieces are tough for students, to connect those pieces back together into a larger whole. That’s some of the most important and most challenging intellectual work of teaching. The better I get at seeing the hidden elements of learning, the more students I can help find success in math class.

This video from YouTube Science Explainer channel Kurzgesagt says a lot of the things I would say about “AI” in this moment, namely: At first it seemed cool, but then it quickly became apparent that the version of it presented to consumers as a creative tool was both deeply flawed and also based on the theft of work from literally millions of creators (including myself!). The bullshit it is generating is now quickly eating the Internet, to the detriment of the actual creative people who make their livelihoods there and also to the detriment of, you know, truth and facts.
In the video, the folks at Kurzgesagt outline how they will and won’t use “AI” — basically not for writing or factchecking, but occasionally for things like automating animation processes and other such backend stuff. I think this is reasonable — and indeed, if one is using creative tools more involved than a pen and a piece of paper, “AI” is damn near unavoidable these days, even allowing for the fact that “AI” is mostly a marketing phrase for a bunch of different processes and tools which in a different era would have been called “machine learning” or “neural networks” or something else now horribly unsexy.
This is also how I’m approaching my writing here on Whatever. Every word you see here is written by an actual live human, usually either me or Athena, but also the individual authors of the Big Idea posts. Good, bad or indifferent, it came out of someone’s skull, and not out of a prompt field. I do this because a) I care about the quality of the posts you see here, and also b) as Athena and I are both actually decent writers with substantial experience, it’s easier just to write things ourselves than to prompt an “AI” to do it and then spend twice as much time editing for facts and tone. That’s right! “AI” doesn’t make our writing job easier! Quite the opposite in fact!
(Also: I don’t use generative AI to create images here — there are a few from years ago, before it became clear to me the generators were trained on copyrighted images, and I stopped when it was made clear this was done without creator consent — so images are almost all photographed/created by me (or Athena) directly, are non-AI-generated stock images I have a license for (or are Creative Commons or in public domain), or are publicity photos/images which are given out for promotional purposes. I do often tweak them with photo editing tools, primarily Photoshop. But none of the images comes out of a prompt.)
I think there’s a long conversation to be had about at what point the use of software means that something is less about the human creation and more about the machine generation, where someone scratching words onto paper with a fountain pen is on one end of that line, and someone dropping a short prompt into an LLM is on the other, and I strongly suspect that point is a technological moving target, and is probably not on a single axis. That said, for Whatever, I’m pretty satisfied that what we do here is significantly human-forward. The Internet may yet be inundated with “AI” slop, but Whatever is and will remain a small island of human activity.
— JS
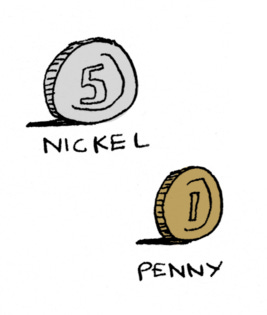
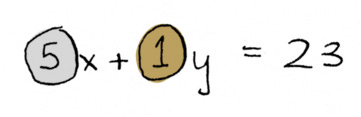
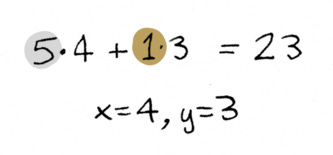
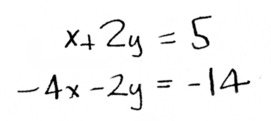
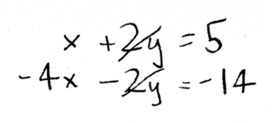
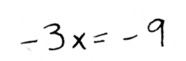
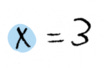
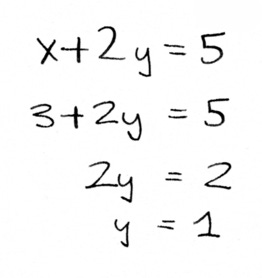
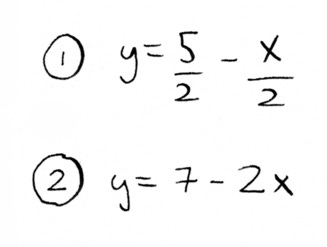

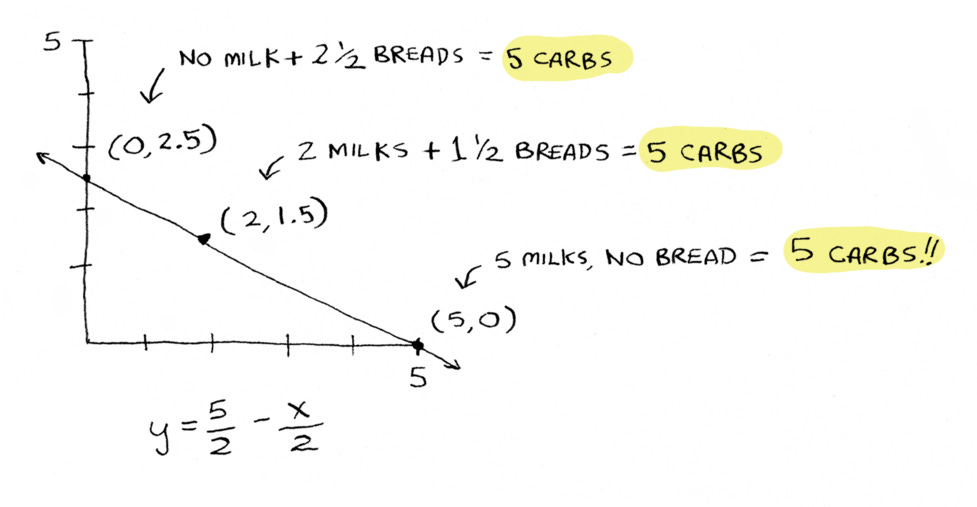

![x * [[1] [2]] + y * [[2] [1]] = [[5] [7]] x * [[1] [2]] + y * [[2] [1]] = [[5] [7]]](https://substackcdn.com/image/fetch/$s_!uQbi!,w_1456,c_limit,f_auto,q_auto:good,fl_progressive:steep/https%3A%2F%2Fsubstack-post-media.s3.amazonaws.com%2Fpublic%2Fimages%2F1c3a203f-b553-4f58-b07f-0136742bf863_398x172.png)

![3 * [[1] [2]] + 1 * [[2] [1]] = [[5] [7]] 3 * [[1] [2]] + 1 * [[2] [1]] = [[5] [7]]](https://substackcdn.com/image/fetch/$s_!iADK!,w_1456,c_limit,f_auto,q_auto:good,fl_progressive:steep/https%3A%2F%2Fsubstack-post-media.s3.amazonaws.com%2Fpublic%2Fimages%2Fc16591c4-b38a-4997-92ad-2ca3605e65d7_344x149.png)
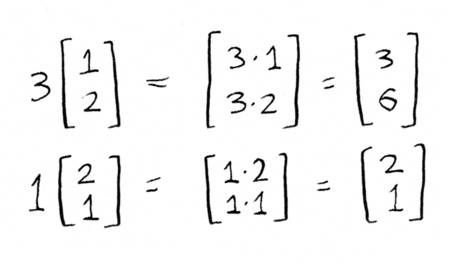
![[[3] [6]] + [[2] [1]] = [[5] [7]] [[3] [6]] + [[2] [1]] = [[5] [7]]](https://substackcdn.com/image/fetch/$s_!ayzR!,w_1456,c_limit,f_auto,q_auto:good,fl_progressive:steep/https%3A%2F%2Fsubstack-post-media.s3.amazonaws.com%2Fpublic%2Fimages%2F6cdc4eaf-8a67-4128-8189-3bbda4f3ad3d_291x491.png)