Your brain is a tool very much like your hands are tools. You use them like tools to do things, even if most of the time you do it instinctively, as if they were givens. Only when you lose their control—a hand injury, a time of extreme mental fatigue or stress—might you realize that these were actually the best devices in your toolbox.

You could say that, to some extent, most of your appendages and muscle-controlled organs are tools in a similar way. But hands and brain are special: they can learn new skills almost without bound and, especially, they can build new tools.

The mind-built tools, or mental tools I return to over and over in this blog are, mainly, framings and models. Although I didn't invent these concepts, I've worked to make them clearer, less ambiguous, and more practically useful. (I have already written a lot about them, so I will spare you the details here—if what follows is confusing to you, you might want to visit some of those links first.)

Knowing framings and models in this enhanced form is a good idea, I think, because they get to the core of what it means to "understand" anything, because they can help you debug your thoughts, and because (among other things) they express how some people can suffer and even die from mental causes.

The main thing I'm working on now (besides the long-overdue final installment of my Purpose Trilogy... almost ready!) is how to make these concepts of framings and models more convenient in practice. Theory and understanding are nice and all, but how do you use these ideas in your daily life? My current question is, can we visualize them?

Two weeks ago we saw that one way to do that is to tinker with the boundaries. But that is a ten-thousand-foot view of things, and there is a limit to how much detail it can handle. Let's try something else. It turns out that visualizing framings is surprisingly straightforward.

First, I'll show you a way I propose you can draw framings and models, then I'll give you a very quick tour of real-world examples in three categories: what business books sell as "mental models", what science calls "models", and how we think about mundane things of (apparently) different domains.

This approach is work in progress and a little rough around the edges. Email me your thoughts on how to improve it!

Visualizing Framings

In short, a framing is the definition of a set of "things" that "exist"—what I call black boxes—and everything else is taken not to exist at all, at least while you're using that specific framing. In other words, a framing is a deployable metaphysics or ontology.

I'll show you plenty of practical examples later in this post, but let's build this gradually.

The obvious thing to do is to treat each "thing", each black box, as a literal box.

It's equivalent to saying, "this is its own thing, separate from the rest of the world, and it does stuff in a somewhat well-defined way."

A black box usually has some properties that we use to describe it, so we write those inside a box.

Some black boxes will also have an intrinsic behavior or mutability that happens on its own, without being induced by the interaction with other black boxes. Remember that black boxes are so called because we choose (or are forced to) ignore what happens inside them. If you look closely, this mutability usually results from interactions of smaller components within and around the system, but those details fall outside the scope of this particular framing, so we treat them as a mysterious "behavior".

Finally, every black box interacts with the other black boxes in its framing in various ways. The exact mode of interaction depends on many things. In truth, it depends on too many things to hope to keep track of them all in one's mind, but that's not a problem. This is precisely what framings are for: simplifying reality by ignoring all but the most relevant interactions.

You could represent this interface as a small set of predefined ways in which that black box can relate itself with other black boxes. These aren't outputs or inputs of the system: they are a catalog of the interactions that you consider possible in the scope of the framing.

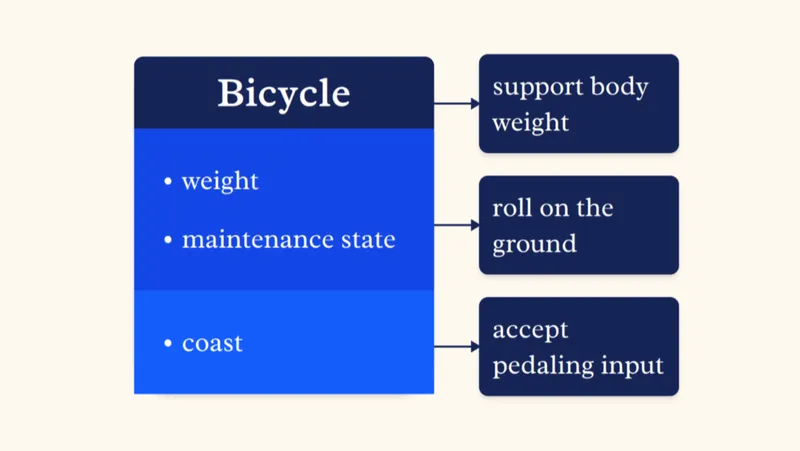
That is all you really need to think about a "thing" in your mental simulations of the world. But the examples above might leave you with a bad taste in your mouth. Surely there is a more rational and effective way to model a bicycle, you might be thinking. There are more factors to consider, and probably there are better ways to structure the problem for easy solution. I agree! I'm not saying that this is the optimal way to think about this or any other specific situation: I'm saying that this is roughly how our brains do it automatically and inescapably because of their fundamental structure and composition.

The limitations of this way of building framings are the limitations of the human mind.

Visualizing Models

Models are just configurations of the black boxes that exist in a framing. Think of a framing as a collection of types of bricks, and of a model as one of the nigh-infinite structures you could build with those types of bricks.

If a framing is about defining what exists, a model is a specific way in which things that exist actually interact and interface with each other. So some people might have an ultra-simplified model of a bicycle's movement:

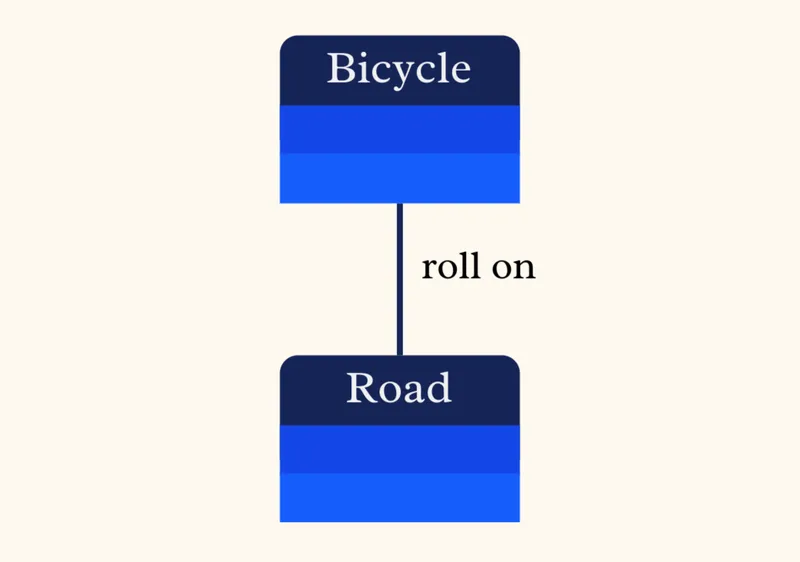
Others, perhaps those more familiar with cycling, might have a model that takes into consideration more interactions.

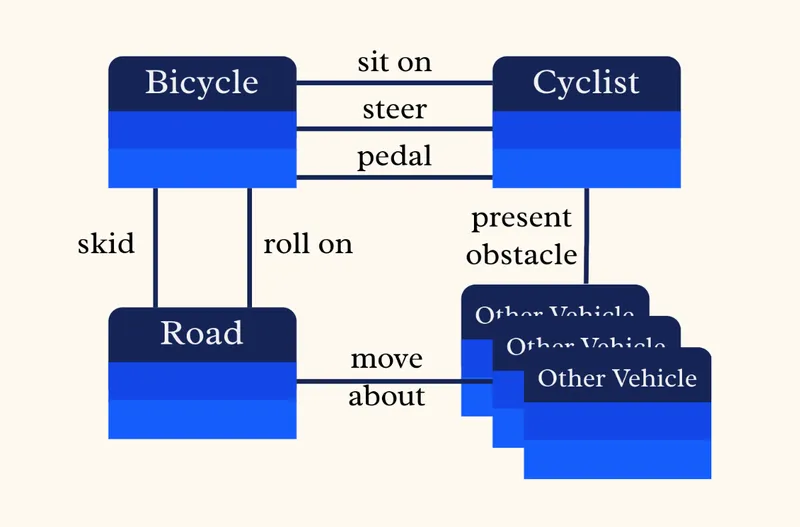
There is no predefined or correct way to model a given situation. Depending on what you know, what you remember, and what you care about at a given time, the level of sophistication of your models will change. The healthy tendency, I think, is to simplify them as much as you can get away with it.

The problem with this kind of visualization is that it is so easy it is boring. This is such a basic function of our brains that all of this seems obvious—not which exact model is perfect for a specific goal, which is not obvious at all, but the fact that there are some ways to connect things in your mind.

For this reason I will avoid drawing this kind of model diagrams in most of the practical examples below. Once you see how the framing is defined, plausible models built on it will promptly pop up in your mind. The juice is in the framings.

Examples: Commonly Cited Mental Models

Occam's Razor

One of the oldest and best-known mental models, powerful and memorable for its simplicity: when faced with two competing explanations for the same phenomenon, the one that makes the fewest (or simplest) assumptions is more likely to be correct.

What this does is create a two-element framing: a world in which there are these black boxes called "explanations" and these other black boxes called "assumptions", and they connect through the relation "based on".

Connect an explanation's interface plug to that of one or more assumptions, and you have a model:

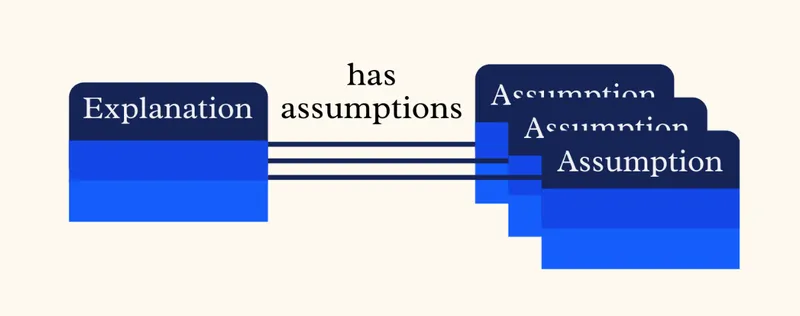
That model tells you that the number and complexity of the assumptions underlying an explanation determine how likely that explanation is to be correct. For this judgment, nothing else matters: not even the exact contents of explanations and assumptions! They are true black boxes for Occam.

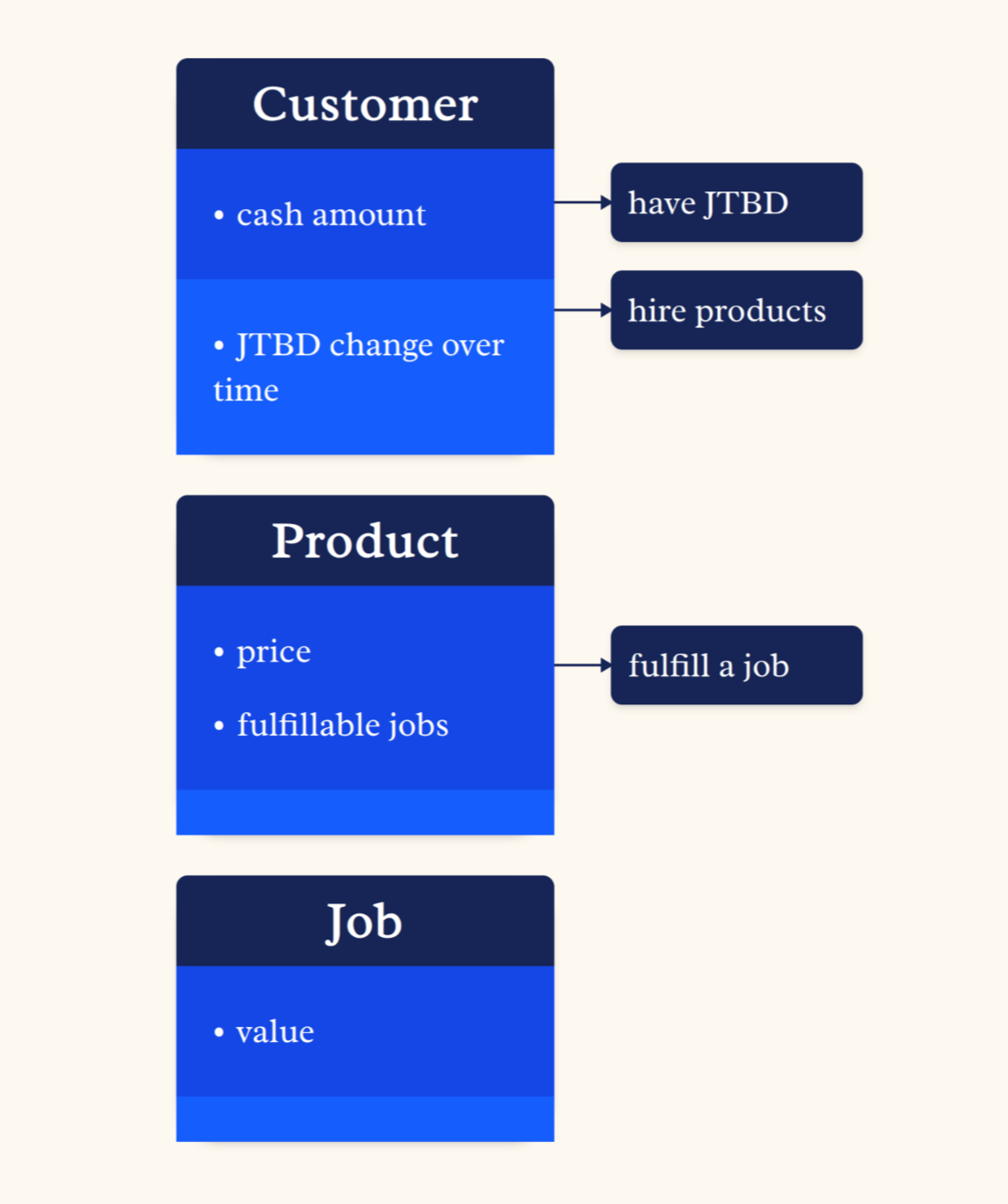
Jobs to Be Done

JTBD is a neat mental model proposed by Clayton Christensen to think about business. It shifts the focus from who a customer is or what product they buy, to the underlying "job" they are trying to accomplish. People "hire" products and services to get a job done.

A person doesn't buy a drill bit because they want a drill bit; they hire it to create a quarter-inch hole. A fast-food chain might realize people aren't just buying a milkshake (the product), they are "hiring" it to make a long, boring commute more interesting (the job).

This shift can lead to ideas that wouldn't otherwise come up. For example, the traditional, pre-JTBD framing probably looks something like this.

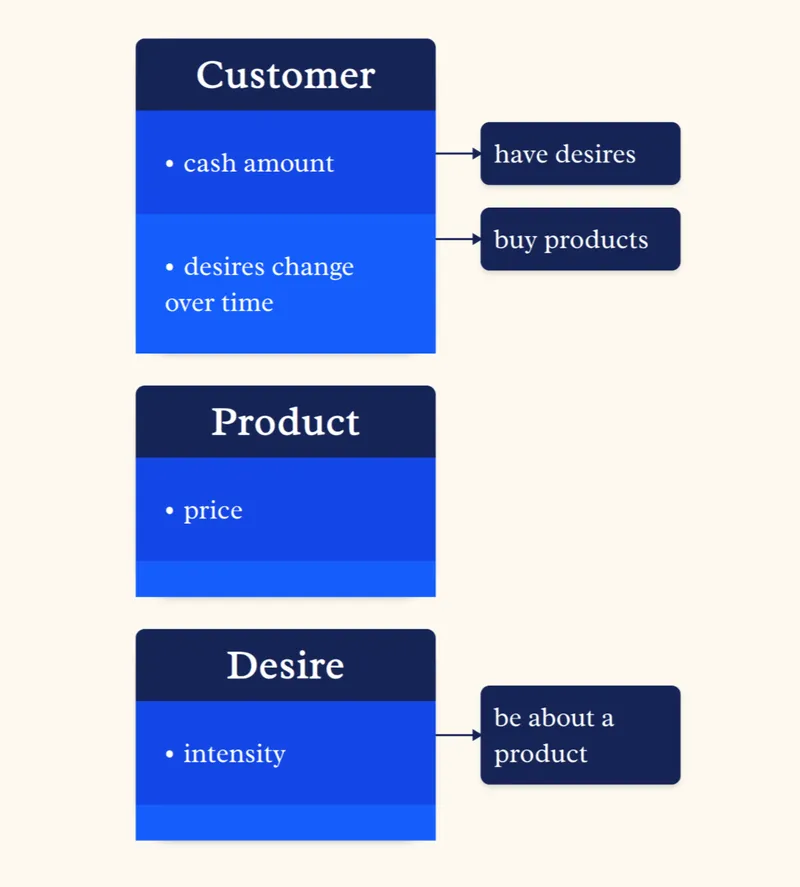
Suppose you wanted to increase sales of, say, your milkshake. In this framing, you might think about tweaking the milkshake's flavor and price to make it more desirable. This might work, but often it doesn't.

Jobs to Be Done uses another framing:

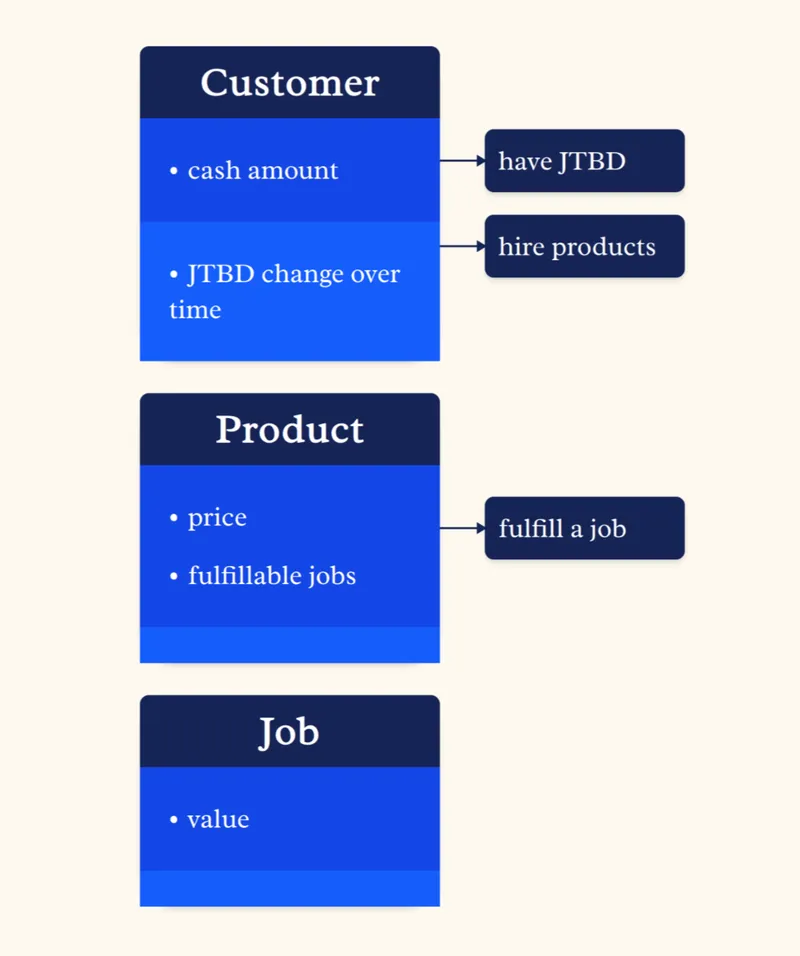
The models you build in this framing may look similar on the surface, but they are not. Whereas before the focus was on the product's qualities, now it is about how the product can fulfill a specific job—how it solves a practical problem. In the milkshake example, where you realized that the job it is usually hired for is to kill time during a long commute, you may consider making the milkshake thicker so that it lasts longer (this is an example Christensen himself used).

The milkshake's thickness would not be the first thing you consider when thinking about its desirability. By adding this new black box called "job to be done" to your ontology, though, the same idea may become almost obvious. This is a mental model doing its job.

Try It Yourself

It's actually quite fun and instructive to figure out what framing and model (as defined in this blog) is employed by any of the popular "mental models" floating around on the internet. For example, take this post by Gabriel Weinberg and go through his list of mental models. What do they define as "things that exist", and how do they arrange them together in ways that change how you think?

You'll notice immediately that, lacking a clear definition of what they mean by "mental models", those lists tend to be uneven patchworks of qualitatively different things. Some of those "models" on Weinberg's list are not complete framings but single black boxes, presumably meant to be added to existing framings or carved out of the forgotten "rest of the world". Others are suggestions of new boundaries to draw inside existing black boxes. I think that the clarified definitions I provided should make the roles and proper applications of these different beasts more intuitive.

Examples: Scientific Models

Models in Physics

Science is the realm of mental (and non-mental) models-as-tools. Most scientific work is about the conscious choice of framings and processes to build, vet, and select the best models inside them. This is a very deliberate, systematic way to work with models. Indeed, it was probably scientists who first created the black box called "model" in the first place.

If you've ever taken a high-school physics class, you have used models in this way, too. You might have solved a problem like the following.

A car is traveling down a straight road at a constant velocity of 10 m/s. The driver then presses the accelerator, causing the car to speed up at a constant acceleration of 2 m/s² for a duration of 5 seconds.

(a) What is the final velocity of the car after those 5 seconds? (b) How far has the car traveled during this 5-second period of acceleration?

This is usually solved by framing it like this:

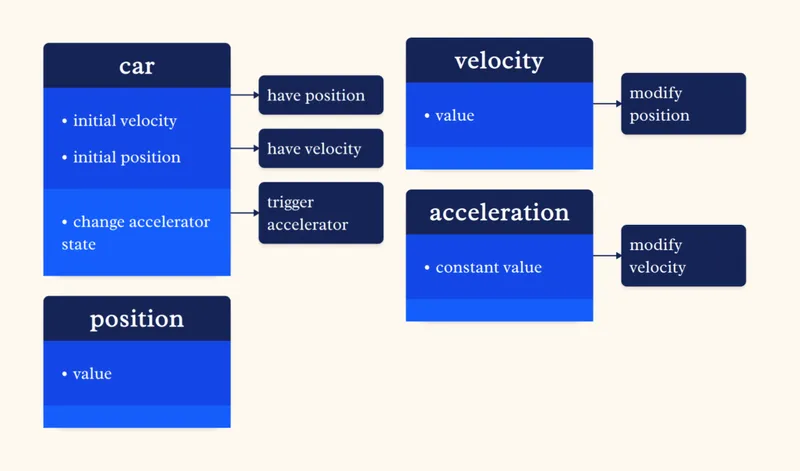
This framing is complex enough to solve problems with constant acceleration like the above, and you can also use it to build models of objects with "piecewise-constant" acceleration, i.e. where the acceleration is constant at value A for some time, then instantly changes to a different constant value B, and so on.

If you have problems where the acceleration changes continuously in more complicated ways, however, this framing will fall short. To solve those, you'll have to introduce black boxes like integrals and derivatives.

More advanced topics, like materials science, quantum physics, and general relativity, all proceed in this same way. The difference is only in that they handle more complex and counterintuitive framings to solve their respective problems.

It's a bit ironic. This core activity of physics—creating appropriate framings to answer questions—is squarely in the realm of "art", not "science". There is no predetermined, "right" way to frame a system, and finding those that are good enough is a matter of trial, error, and intuition. Fortunately, for all but the most cutting-edge fields, textbooks offer vast catalogs of pre-built framings to reuse and tweak as needed.

Examples: Everything Else

Up to now, you might still be clinging to the idea that framings and models are specialist tools used knowingly in jobs like marketing and research. But no. Consciously or not, we all use framings and models for every single thought we think. We can't think in any other way.

The best way to see that is looking at what psychologists and philosophers call "folk science"—the intuitive, implicit understanding of how the world works that we all have since infancy.

Folk Physics

Even toddlers know a range of physical "laws" that allow them to interact with the things around them and make certain modest predictions. These form a set of empirically-known framings that doesn't need to be taught, and we all carry them in our minds even as adults. Some of us, over years of education and work, learn to improve them or replace them with more advanced and powerful framings and models, but that is less common than you might think.

For example, people intuitively believe that objects thrown upward will always fall back down. In other words, a simple black box like this:

This framing works just fine in most everyday situations, even though it is pre-Newtonian in nature. But if you expand the scope of application—e.g. very high velocities—it will stop working. The concept of "escape velocity" doesn't exist in this bit of folk physics, and someone will have to teach you a better framing to handle that.

Folk Biology

People generally believe that belonging to a species is determined by descent:

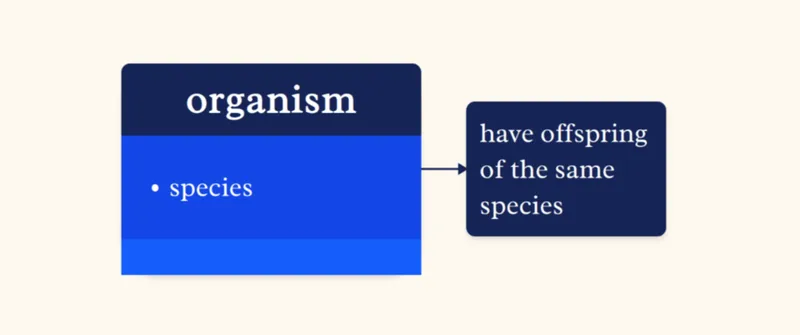
In most cases, this is a reasonable assumption. But if this were really true, how would new species begin?

As Daniel Dennett explains well in his book Darwin's Dangerous Idea, new species are surprisingly difficult to pin down because they only make sense in a retrospective sense.

Speciation ... has a curious property: you can’t tell that it is occurring at the time it occurs! You can only tell much later that it has occurred, retrospectively crowning an event when you discover that its sequels have a certain property.

Each offspring is always extremely similar to its parents, except for a few tiny mutations here and there. It is only after those offspring have lived their lives, and their offspring have lived theirs, and so on for a while, that we can tell if any given mutation turned out to be a key differentiator of a budding new species. Dennett clarifies this with an analogy:

Other concepts exhibit similar curiosities. I once read about a comically bad historical novel in which a French doctor came home to supper one evening in 1802 and said to his wife, "Guess what I did today! I assisted at the birth of Victor Hugo!"

To understand speciation in a less "folk" and more scientific way, you need a bigger framing where, alongside the "organism" black box, you have other black boxes like "population" and "lineage".

(By the way, improved framings like Dennett's lead to a fun realization: you and everyone you know is yet another attempt at starting a new species. Will you succeed?)

Folk Psychology

When you see someone reaching for a glass of water, you intuitively infer they believe the glass contains water and desire to drink it. This attribution of mental states to explain behavior is a typical example of folk psychology, our intuitive approach at making sense of other people.

Folk psychology (and theory of mind) tends to be more complex and fuzzy than those neat physics problems, for obvious reasons. Your implicit framing for the scene above might be something like this:

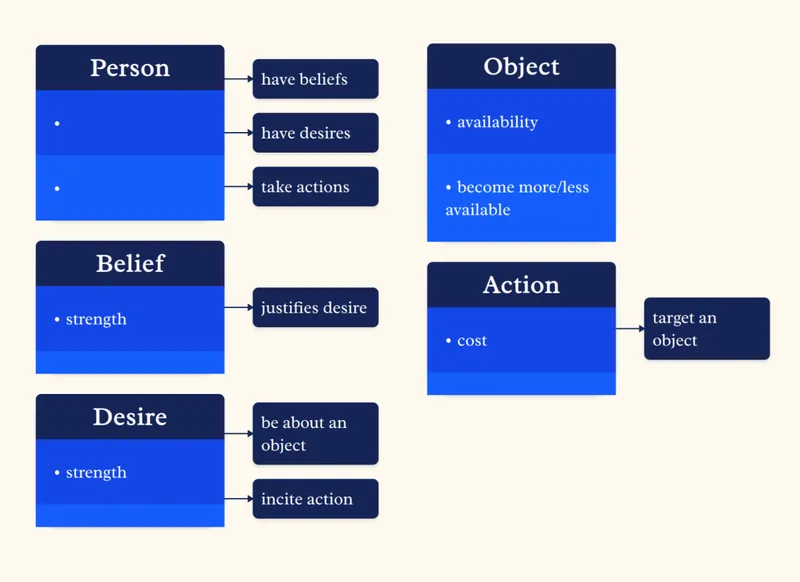
If words like "belief" and "desire" seem perfectly natural and clear to you, ask yourself: where are they? What are they made of? There are no "belief neurons" or "desire neural networks" in the human brain. People have looked. These concepts are artificial boundaries that we created to delineate convenient black boxes for our explanations of the world.

But folk psychology creates the risk of what I call Tunnel Vision—forgetting that you're using a simplified framing of the world, and consequently becoming trapped inside it. It's when you believe that people have to behave in certain ways, and that you just can't break free of certain conventions that society has imposed on you. Almost as if those were laws of physics.

It's All Just UML

If you have a technical background, you may have noticed that the diagrams I drew above are eerily similar to Unified Modeling Language class diagrams. UML diagrams are are more complex and have more moving parts, but they are essentially the same as those I've been drawing.

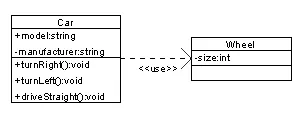
So am I stealing ideas from engineering? Yes! In a Robin Hood way, though. When James Rumbaugh invented this way of representing the relationships between entities, he was thinking only about software architecture. The problems his team was trying to solve were about designing the relationships and interactions between many parts of large computer programs. But what they discovered had a much broader applicability than they seemed to think. Wouldn't it be nice if all the visual tooling and methods they built for a specialized sub-discipline turned out to be useful to better understand how the mind works? ●

Arguably, the golden age of browser gaming occurred in the 00s mostly revolving around Adobe Flash. This was an era with high creativity and a low barrier of entry, and also decentralized from gatekeeping app stores. Sadly, these times have passed us by as the security concerns around Flash led to its discontinuation and most casual gamers have migrated to the app store for their fix. But that doesn’t stop some from continuing to bring gaming to the browser, even if those games were never intended for it in the first place like this browser port of Celeste.

Celeste is an indie platformer where the player climbs a mysterious mountain while confronting her inner struggles. Originally meant for consoles and PC, a group of friends including [velzie], [bomberfish], and [Toshit] aka [r58Playz] took this as a challenge especially after seeing someone else’s half finished web port of this game. Most of the build revolves around WebAssembly (wasm) and around “cursed” .NET runtime hacks which also allow the port to run the community-made Everest mod loader. It uses a multithreaded and JIT compiling version of mono-wasm backported from .NET 10 to .NET 9 to maximize performance. The team actually first started by porting Terraria to the browser, and then moved on to this Celeste port from there.

The port of Celeste can be played here, and their port of Terraria is also available, although may not support a ton of Hackaday traffic so some patience is advised. There are also GitHub repositories for Celeste and Terraria as well.  With impressive ports of relatively modern games moving into the browser, perhaps we’re entering a new golden age of browser gaming; we’ve also seen things like Minecraft implemented in only HTML and CSS lately as well.

I don’t believe in ghosts. This is not a story about ghosts. But if you want to see a ghost, I can think of no place more promising than Baby Head Cemetery, where I am pretty sure I almost saw a ghost.

Last November, I loaded my dog, Woody Guthrie, into the truck for a day trip from Austin. The rain starts as I head out of town, and the low-hanging clouds feel right for this mission. On State Highway 16, just north of Llano, I pull up to Baby Head, a place I did not make up in my nightmares. But to double-check my sanity, I read the Texas Historical Commission marker. Everything I’ve read online about this place—the hill, the community, the cemetery—quotes this marker, which puts the blame for the haunted name on oral tradition. The story goes that after a raid by Native Americans in the 1850s, an Anglo child’s remains were found on the so-called mountain.

It’s pouring rain, but my dog’s happy to get out of the truck and stretch his legs after the drive. I’ve already decided I don’t want to be here. I’d come here to see a ghost town—and this is not a ghost town. But it feels disrespectful to just leave.

We head to the grave markers. About halfway down the little path, my dog stops. I call him. I tug his leash. He doesn’t budge. He lowers his head and employs the superpower every dog channels at the door of a veterinary clinic: He becomes an immovable object. Then, he starts whining. I admit, he’s had his moments of stubbornness, but this isn’t normal.

Listen, all that stuff I said about ghosts is true. I’m not a person who believes in things, least of all ghosts. But when you’re standing in a graveyard and there’s no one around, the wind is howling and it’s getting dark, and then your dog turns into a stone … I don’t want to admit this, but I feel a shiver run up my spine.

Hanging out in a graveyard makes me reconsider my belief system, or lack thereof. Maybe the ghosts don’t care what I believe. I look around. For what? I don’t even know. Then Woody Guthrie, realizing I’m a moron, lifts a front leg to show me the problem: His paws are full of stickers. I apologize to the ghosts I don’t believe in because it never hurts to be polite, and I carry him back to the truck.

I’ve always loved a ghost town. Maybe it’s because I’m a fan of history. Maybe I’m just nosy. But I’m obsessed with seeing how people used to live, imagining the stories in what they leave behind. I can see a ghost town in my mind—dusty old buildings, crumbling bricks, sun-bleached boards, and signs blasted clean by the wind. A general store. A railway depot. A courthouse. A jail. Maybe a saloon. Off the main street, a few houses in varying states of decrepitude. I don’t know where the images come from. Movies maybe, or pictures in a magazine. Because I can’t think of a single ghost town I’ve visited, though not for lack of trying.

I went to Marfa a couple of years ago, and while I was there, I saw a little dot on my map for a town called Shafter. Wikipedia told me Shafter was indeed a ghost town, an old silver mine 20 miles north of the U.S.-Mexico border. But when I got there, the place was fenced off and marked with No Trespassing signs in a manner that looked like someone was serious about it. I was surprised to find myself sad that I couldn’t walk around. The next ghost town I visited was Terlingua. You say “ghost town” in the vicinity of Austin or Marfa and someone will ask if you’ve been to Terlingua. But the day I went, it was crowded and the bar was open.

I take a lot of road trips. And I’ve pinpointed at least 20 purported ghost towns on my map, mostly up in the Panhandle, bearing names like Machovec, Electric City, Middlewell, Tascosa, and Bunker Hill. I’d drive to the spot on the map. Look around. Drive some more. Take a left this time instead of a right. And every time, I’d find nothing. Shouldn’t be hard. I can see 50 miles into the distance. But any direction I looked, there was nothing but farmland. Not even the ghost of a ghost town.

I’ve seen plenty of abandoned farmhouses alone in the distance or right by the highway. Well ran dry. Mine went bust. Bank took the land. People moved on. Or, as I  imagine, they built another house somewhere, planted a few trees, and hung a tire swing.

I want to see a real ghost town, but clearly, the internet can’t be trusted to identify one. So, I call T. Lindsay Baker, a retired history professor at Tarleton State University and author of Ghost Towns of Texas and More Ghost Towns of Texas. I start with the basics: “What is a ghost town?”

“A ghost town is a town for which the reason for being no longer exists,” Baker says. He had three criteria for a town to be included in his travel guide. One, there must be some tangible surface-level archeology. “It’s no fun to drive out to what turns out to be a paved parking lot,” he says. Two, the town has to offer public access. And three, there must be even geographic distribution, so
wherever you are in the state, you can easily visit a town on a day trip. He didn’t specify a population other than to say fewer than 100 people sounds right.

Baker identified more than 1,000 towns in Texas that met the three criteria. And they’re all over, not just here. “It’s the nature of the United States,” he says. “The stereotypical ghost town is a mining camp. The mine goes bust when the minerals run out or when the market for those minerals disappears. So, people move on.”

I tell him about trying to see Shafter and how it was fenced off. “Oh, that happened to me scores of times,” he says. “You have to have surface archeology. Hard to find a ghost town without it.”

I think of the time I tried to find a ghost town called Gay Hill, just north of Brenham, in Washington County. I’d seen pictures of Gay Hill—the general store and the cotton gin. According to the Texas State Historical Association, a post office opened there in 1840. But in 1881, the railroad established a stop 2 miles away and the town was moved. The old town was renamed Old Gay Hill. After World War II, with the decline of cotton, the town dwindled. By 1971, it was all but empty. Still, there’s a dot on Google Maps that says “Gay Hill,” and it was only a two-hour drive from Austin.

I filled up my tank, grabbed my notebook, and headed out. I drove around for an hour at least, in a downpour. Up and down State Highway 36 and Farm-to-Market Road 390, and every road and lane that met 36 and 390. I found a farm, another farm, a few fences, more farms, and nothing more.

The first week of March, Woody Guthrie and I head west. The sky’s candy blue, and there’s a cloud of dust up ahead. When we hit the first dust storm, I think maybe we should’ve waited another week. It’s just a little squall, though. The world disappears for a moment, and you’re through. Then, we hit the big one. In a couple of years, I’ve gone from seeing no dust storms, and now we’re at four dust storms, three in one day. The world is sepia toned, and I’m not sure we should keep driving.

By the time we get to Toyah, about 20 miles southwest of Pecos on Interstate 20, the wind’s howling and there’s still dust flying. It’s annoying but not apocalyptic—perfect ghost town weather. It seems I’ve found a real ghost town, the way I want a ghost town to look, sandblasted and lonely.

Toyah started as a trading post in the 1880s, boomed after the railroad came through in 1881, and peaked at 1,062 residents in 1914. But apparently the railroad moved, and even a small oil boom in the 1920s couldn’t save the town. By the Great Depression, the population had dropped by half. The grocery store is thought to have closed in 1940.

There’s a massive brick school building at what looks to be the center of town. The wind’s pushing a swing out front and rattling what’s left of the metal roof. I walk the deserted streets with Woody Guthrie, both of us squinting against the dust. Floods and a reported tornado took their toll. Piles of bricks are all that’s left of one building. Others, you could see a hipster turning into an overpriced ramen shop with some paint and a new roof. Cars sit on rusting frames, and the requisite bathtub lounges beside what’s left of a window.

I can’t get over the feeling I’m trespassing. I’m not, to be clear. But it’s strange to look through the window of what used to be someone’s house, someone’s business, someone’s hopes and dreams. Woody Guthrie has no such qualms. But I keep him close. A car passes, and I realize what’s bugging me. This doesn’t feel like a ghost town. People still live here—but only a couple dozen. No wonder something’s not right. Or maybe it’s just the howling wind.

Barstow, east of Pecos, is the next ghost town on my itinerary. Again, though, it’s a ghost town that’s not quite a ghost town, or not how I imagined it. Barstow formed in 1892 and was largely abandoned after droughts in the early 1900s. A bank that says “Bank” on it remains on a corner, but the roof’s long gone. A pile of dust is stacking up against the remains of the Modern Food Market. Up the street, a truck pulls out as I’m pulling in. A guy in a felt hat waves at me, and I wave back. But I’m not the sort of person who can go knocking on doors, asking questions like, “Where did everyone go?”

I’d probably get some great answers if I could do that sort of thing. But I cannot. What I do instead is I complain to people. The trick is to complain to the right people. The first right person I complain to is Jac Darsnek, who runs Traces of Texas, a history-themed Facebook page with more than 1 million followers.

Darsnek sends me a photo he took in Barstow circa 2007. “I was taking this photo when an older gentleman in a beat-up pickup truck drove up, stopped, and said, ‘We just had a meeting at the coffee shop and decided we’d sell the whole thing to you—kit and kaboodle—for $117.82,’” Darsnek says. “I smiled and asked, ‘Why the 82 cents?’ He said, ‘Because that’s how much a cup of coffee with tax costs over there.’”

I reconsider talking to the ghosts I don’t believe in, but then my complaining pays off yet again. A family friend, probably tired of hearing me talk about ghost towns, looks at her husband and says, “Don’t we know a guy who bought a ghost town?” That’s how I am introduced to Blair Schaffer and his wife, Blanca.

Blair gives me directions to Jericho and says he’ll meet me there. I head up to Amarillo and go east on Interstate 40. A little past Clarendon, I get off on State Highway 70. Blair’s truck is idling on the side of the road. He gets out as I pull up behind him. He waves and shouts “Hi!” then “Lauren?”—though mine is probably only the second truck on this road all day, and his is the first.

I follow him to Jericho. Once we’ve parked, Woody Guthrie’s out of the truck like a shot, chasing smells or ghosts of smells. He doesn’t care. This was the destination he expected. Me too.

Blair walks up in square-toe boots and a glorious red mustache. Blanca’s black hair is whipping over her face, so she ties it back. I get right to it: “How and why on earth do you buy a ghost town?” They both laugh, and I add, “I guess y’all get that question a lot.”

Blair’s a fireman in Amarillo and a Potter County commissioner. Blanca’s a history buff. They always talked about buying a little land as a homestead, somewhere they could retire, something they could pass on to their kids. In 2020, the gym they owned in Amarillo was hurting due to COVID, so they started looking for land. That’s when they saw Jericho come up for sale. In the late 1800s, Blair’s family moved to Jericho from Missouri in a covered wagon. “We used to come out here when we were kids to visit their graves and clean up the cemetery,” he says. “I’ve been coming to Jericho my whole life.” When the land was posted for sale, they knew it was meant to be.

The sun reflects off an old school bus as we walk into a light breeze. Up ahead, there’s an L-shaped building, the old Reeves Filling Station and Motor Court. The rooms are intact, but the roof’s caving in and the doors are missing. There’s a bed frame and wallpaper in one room, a chair in another. At last, I feel like I’m allowed to poke around.

For a long time, this land, first settled by buffalo hunters, was nothing more than a trading post. But in 1902, the railway established a station in Jericho, and in 1926, when Route 66 was commissioned, the town became a real town, complete with a service station and this tourist court.

Blair points out how they used the old saw blades from the mill as rebar in the concrete, and Blanca shows me a safe they pulled from the dirt. Blair says they’ve decided it must be a safe Bonnie and Clyde stole. It’s empty, but that only proves their theory as far as I’m concerned.

We come to the outline of another building, but this one has a basement. “That was the birthing center,” Blanca says. “A midwife would’ve lived in the house. And if you were giving birth out here, a little far from a hospital, you’d come here to have the baby.” The building’s long gone, but the irises planted in the yard over 100 years ago are in bloom.

Blair shows me the pit generator they found buried, which would’ve powered the buildings. What’s left of a shower still stands behind a house—so the people who lived here could wash up after work without tracking in dirt.

I’m so lost in these details, I realize it’s been too long since I’ve seen Woody Guthrie. Blair spots him running up the dirt road, back from chasing something he probably shouldn’t. Blair says that’s the old Route 66, and I think he’s kidding. “This part was unpaved. It was called the Jericho Gap,” he says. “Mostly it was fine. But if it rained, it was unpassable. So, people would have to wait it out in Jericho.”

The Schaffers show me where they plan to build, the gardens they’ve started, the roof they’re trying to save over the tourist court. They want to rebuild the old hotel as a museum. To raise funds, they host ghost tours, hayrides, and even a 10K race. They offer stargazing nights and welcome RVers to camp. They may have planned a homestead, but what they’ve found is a mission—to save Jericho.

We look out at the sun setting across the fields, standing where their living room will be someday. “This is it for me. I found my place,” Blanca says. I’m glad the Schaffers are here now, to preserve their family history and to tell us the story of a true ghost town.

Funny how I went looking for something haunted, but what struck me—what made the ghost town come alive—was the people I met on this little quest. “Texas ghost towns began as a dream, an idea, a response to opportunity. People came chasing something,” Darsnek reminds me.

People like me see a ghost town as a curiosity, a reminder of the past, while the Schaffers see it as an opportunity. They see their dream coming alive. If a ghost town is a town without a purpose, I don’t know that Jericho qualifies anymore. I can’t think of a better purpose than fulfilling a dream. 

The post The Quest to Resurrect a Ghost Town appeared first on Texas Highways.

I've recently been experimenting with one of my favorite old-school neural networks, a tiny program that runs on my laptop and knows only about the data I give it. Without internet training, char-rnn doesn't have outside references to draw on (for better or for worse) but it still manages to remix the data into interesting new things.

In 2017 I asked AI Weirdness readers to help me crowdsource a list of Halloween costumes and then trained char-rnn on the nearly 4,500 submissions I got. Today I'm returning both to the dataset and to char-rnn (here's a version that runs on modern Python), mainly because they still entertain me. My laptop is more powerful now than the 2010 Macbook I was using back then, so I'm able to run a bigger version of char-rnn. I actually can't tell whether it helps. But I do know I'm entertained:

The Skypug
Hungry Boats
Mid wonka
Burderous bread cat
Holy Cheesarenda
Moth fairy
A magicial slice
Fall wearing monster
The Godfish

I checked, and nobody in the training data from 2017 was using "mid" as an adjective, so "Mid wonka" is a happy coincidence. The larger version of char-rnn was better than I expected at remixing costumes, producing interesting new characters.

science horse
Lady Doo
Captain Gay
Silence Minister
Cheetos Captain
A scorph Doo
Undead Mario
Sailor Who

There were a couple of Scooby Doo costumes in the original training data, which is probably why the neural net is putting doo in its costumes.

Know what was not in its 2017 era training data? Kpop Demon Hunters, which I have it on good authority will not be an unknown costume in 2025. For fun I asked the neural net to complete the phrases "Kpop " and "Kpop D" and "Kpop De":

Kpop Punk
Kpop and the man and a bus
Kpop Bader Ginsburg
Kpop Dog
Kpop Donald science
Kpop Devil Monster
Kpop Dead Death
Kpop Demetic
Kpop Dead of Turtles

This holds for larger language models like ChatGPT as well, of course. If a current event or a perspective is missing from the training data, it's missing from the result.

The submission form for crowdsourced Halloween costumes is still open, so if you have a few costumes you've seen or dreamed of recently, you can help bring the training data up to date! If I get enough new submissions maybe I'll train the neural network again. (The dataset as of Oct 4 2018 is available on my github).

Bonus content for AI Weirdness supporters: a few more of my favorite costumes trained from the 2018 dataset!

From Catriona Agg’s endlessly rewarding Twitter feed:

The three smaller squares are the same size. What’s the angle? (The outermost shape too is a square.)