By request, here’s a summary of my lessons from the last week. Hopefully this gives a bit more detail to my post earlier this week about teaching with multiple strands.
A quick note about the structure of this post: Below is a basic summary of where I’m at in the yearlong sequence for each of the three strands. Next there’s a quick outline of my class each day this week. Then I give a few notes reflecting on how I structure my class and sequence curriculum. I don’t want to clog up the post with too many details about the nitty gritty of my routines so there are a ton of footnotes. If you want to learn more about all those details, enjoy!
The Strands
I have three main strands of my curriculum this year. This image shows the rough idea:
In the top strand we are almost finished with proportional relationships; this week we’re focused on analyzing graphs of proportional relationships and then we’ll move on to percent increase/decrease in the top strand.1 In the rational numbers strand we’ve finished a big review of adding/subtracting/multiplying/dividing fractions, a lot of practice with the basics of number lines, some work on different contexts where negative numbers come up, and adding positive and negative integers, fractions, and decimals.2 This week we started working on multiplying with negatives. In the expressions and equations strand we are working on one-step multiplication equations. We’ve finished a lot of practice with addition and subtraction equations, including addition and subtraction word problems.
A Few Everyday Routines
Before I get into my week, I have a few everyday routines so students know what to expect at the beginning and end of class. At the start of class I welcome students in, they drop their backpacks in a designated area in the back corner of the room, grab a half sheet for their Do Now, and sit down. Below is one example of a Do Now I used on Tuesday.3
While students answer the questions and try an optional puzzle, I take attendance, make sure everyone has a pencil, and deal with any issues that come up. I aim for three minutes flat for work time. I do a quick circulation around the room, often focusing on one question I anticipate will be the toughest. Then we quickly go over the answers. If there’s one question I see a bunch of students getting wrong, I make a note and return to it when we pull out mini whiteboards in a few minutes.
Next, on the back of the Do Now half sheet, we do an estimation routine.4 Here’s an example question:
The final everyday routine is DeltaMath. DeltaMath is a practice website that offers a lot of customization for teachers. Every day students have a DeltaMath assignment, and we spend the last 5-10 minutes working on these.5 Students finish anything they don’t get to for homework or in a separate study hall period.
Also, note that my classes are 50 minutes long each day. There are a lot of bullets under each day. The timing varies a bit from class to class but in general each bullet represents 5-10 minutes of teaching. We move fast! There’s lots of math to learn, and not much time to learn it.
Monday
On Monday we started with the Do Now and estimation.
Then, I had students grab a whiteboard, marker, and rag to erase with.6 I asked a few quick questions to check understanding of prerequisite skills for the day’s lesson. I write each question on the board, have students answer on their own mini whiteboard, and hold up their boards on my signal so I can see their answers. I checked whether students could identify if a relationship was proportional from a table, whether they could solve a one-step multiplication equation, and if they knew that the name of the point at (0,0) was called the origin. A few students mistook the multiplication equation for addition, so we did a bit of clarification and extra practice with that. This was maybe 5 minutes total.
Next we did a bit of mixed practice on paper with whole-number one-step equations, including addition, subtraction, and multiplication equations.7
Then we launched into a larger chunk of class focused on graphing proportional relationships. I modified an activity from the Illustrative Math curriculum about seagulls eating trash. It’s a bit of a weird example, but was good for building off of students’ knowledge of proportional relationships in tables to give examples and non-examples of graphs of proportional relationships.
Then I had students open up their Chromebooks and try a short chunk of the DinoPops activity on Desmos.8 This is a chance to apply some of what we had just talked about with graphs of proportional relationships.
Next we did some very quick practice distinguishing graphs of proportional relationships vs non-proportional relationships with mini whiteboards.
Finally students finished with DeltaMath. DeltaMath included some mixed practice of addition/subtraction fluency, evaluating percentages, and solving one-step equations.9
Tuesday
On Tuesday we again started with a Do Now and estimation.
Then I had students answer a few questions on mini whiteboards. Some students had answered 0 for -5 + (-5) on the Do Now this day so we spent some time practicing adding negatives and distinguishing between problems that add to 0 and problems that don’t. I also asked students whether a graph of a relationship was proportional and why, I asked again for where the origin was, and another question about one-step multiplication equations.10
Then we did a quick round of multiplication fact practice. This focused on the 11s fact family, which means half 11s and half the other facts we’ve focused on so far which are 2s, 3s, 4s, 5s, and 10s.11
Next we did a handout extending multiplication equations to fractions. The goal was to extend the generalization that you can use division to solve a one-step multiplication equation to division of fractions. This honestly didn’t go that well, so I cut the discussion short and we returned to it the next day.
Next we did a bunch of examples of proportional and non-proportional relationships. Some were about pizza — if you want to make twice as many pizzas, you need twice as much dough and cheese, but you don’t need to cook at twice the temperature. Others were some silly examples I made up about the relationship between the number of people and the number of arms, or students and teachers. The goal was to look at a bunch of graphs of relationships and think about why that graph is proportional or not.
Then we did a five questions check for understanding of adding negatives, focused on questions like -3 + (-3) and -4 + (-4) + (-4), which is relevant to the lesson tomorrow. I followed up individually with a few students who made mistakes during DeltaMath.
Finally students did some DeltaMath focused on questions about graphs of proportional relationships.
Wednesday
On Wednesday we again started with a Do Now and estimation.
Then I did a quick thing sharing the story of Srinivasa Ramanujan. We watched the trailer from the movie about his life, The Man Who Knew Infinity, and I added in a bit more of his story that isn’t in the trailer. We do one of these most weeks.12
Next I did an introduction to multiplying negative numbers. I focused on the idea that 2x3 really means 3 + 3, or 3x4 means 4 + 4 + 4, so the same is true for negatives. 2x(-3) just means -3 + (-3), which we were just practicing yesterday.
Then I had students grab mini whiteboards and we did some practice, with a mix of two positive numbers and one positive/one negative where the negative comes second. I also mixed in a check for understanding on fraction division, and did a quick model of fraction division and some extra practice.
Then we did another handout building up to solving multiplication equations with fractions. This one moved more gradually from simple equations like 10x = 30 to equations with larger numbers, decimals, and then fractions. I did a bit of modeling again, and this went a bit better than Tuesday though students will need some more practice.
Next we did a quick activity adapted from Illustrative Math connecting equations for proportional relationships (which we had already spent time on in the context of tables and word problems) to the graphs of proportional relationships.
Next we did a 10-question quiz, which covered topics from all three strands as well as some review questions from weeks or months previously.13
Finally students did some DeltaMath mixed practice, with questions on adding integers, solving equations, finding percentages, finding unit rates, and some fact fluency.
Thursday
Day four: formative followup, CFU multiplying negatives and formative followup, 11s, multiplication practice, curriculum resources for graphs, stop and jot multiplication, DM focused on equations
On Thursday we again started with a Do Now and estimation.
The most common mistake on the quiz from Wednesday was a question about a snail traveling at 1/2 a foot per minute (students struggling with fractions is a theme this week). We talked about a simpler question with whole numbers, then the snail question.
Next I had students grab mini whiteboards and try two more questions like the snail question, and did a check for understanding of multiplication with negatives (a surprising number of students added on the first one).
Then we did a handout from the JUMP curriculum that focuses on patterns in multiplying negatives and the commutative property, and a handout I made with some practice multiplying negatives. No negative times a negative yet, though. This went really well!
Next was another quick round of practice with multiplication equations and fractions.
Then we did some problems from the Reveal curriculum about graphs of proportional relationships. These went alright, though students had a tough time reading unit rates off of the graphs so we’ll return to that next week.
Next was a five-question check for understanding on multiplication equations. This is still a bit of a mess, need to figure out how to support the students who are having trouble with this next week.
Finally students wrapped up with some DeltaMath focused on proportional graphs, adding integers, and solving equations with whole numbers.14
A Few Thoughts
I’m genuinely curious for people’s reactions when they read this. I want to emphasize that I’m not some huge expert on this type of teaching. I’ve experimented with these ideas for a few years but this is the first year I’ve gone all-in on teaching multiple strands at once. I was doing some of that experimenting last spring during my formal observation, which is also the only time I’ve received substantive feedback on my teaching in the last year. The one piece of constructive feedback was that the lesson felt scattered because there wasn’t one objective.
And sure, if you are a teacher who has only ever taught lessons with a single objective, this feels weird at first. It felt weird to me for a while. But my experience is that it doesn’t feel weird to students. They come to math class, we do math. Most activities are either practice, or taking something we’ve done and taking it one small step further. Is my sequencing and pacing perfect? No, absolutely not, I’m learning all the time.
I find that this style of teaching benefits students in multiple ways. Students who have trouble with focus and sustained attention benefit from the transitions and short chunks. Students who feel frustrated because math is hard for them benefit from spending a few minutes on a topic and then moving on to something different, rather than banging their heads against something for the whole 50 minutes. Students who have stronger skills benefit from the variety — it’s much more interesting to do a short chunk of review of something you already know pretty well mixed with new content than to spend the whole period on it. Students who struggle with long-term retention benefit from the spacing and repeated short chunks of practice.
I’m piecing together a few different curricular resources rather than following one resource. I do that because I’m not happy with the resources my district has adopted. But I think you could do this with any commercial curriculum. The biggest thing you would need to do for most programs is to add in a lot more review of content from prior years, and break the practice down into smaller, more focused chunks.
My motto is “go slow to go fast.” If you’re a 7th grade math teacher, you might read this and say, “wow, you have a lot left to get through this year.” True! While we’ve made some good progress, we’ve spent a lot of time on review and foundational skills early in the year. The goal — and this has mostly been true so far — is that if I take my time with the foundation, then learning the tougher grade-level content will go more quickly and smoothly. I have all the topics mapped out for the whole year. I adjust as I go, but so far I’m within a week of my goal for each of the three strands.
I wrote last year about the motivation fractal.
On the x-axis is time, and on the y-axis is difficulty. The blue ellipse is one lesson. So each lesson has a few activities, each going from simpler to more complex, each starting easier than the last one ended. Then the next day, we get a bit tougher and repeat.
The image above is the ideal. Practical challenges mean that my classes don’t always look like that. But it’s the goal. The reason I made this change to my curriculum is that I just haven’t been successful in past years. Too many students struggle to keep up, feel that the curriculum moves too fast, and don’t have time to build a strong foundation before going on to the next thing. This is the best solution I’ve found. It’s not perfect, but it’s way better than anything else I’ve tried.
If you have questions, please ask away!
In the image outlining the strands I oversimplified. I started the year with basic percentage problems — finding a % of b, what percent is a of b, stuff like that. Then we do proportional relationships, and then percent increase/decrease. This connects well — percentages are a form of proportional relationship. This also gives students plenty of time for retrieval practice with percentages to improve fluency with those questions before we get to the percent increase/decrease and multi-step stuff down the road.
I am sequencing rational numbers as addition → multiplication/division → subtraction. I’ve found that subtracting with negatives is one of the toughest topics for students, and the goal is for students to get really fluent with addition first to build confidence and set up a strong foundation for subtraction.
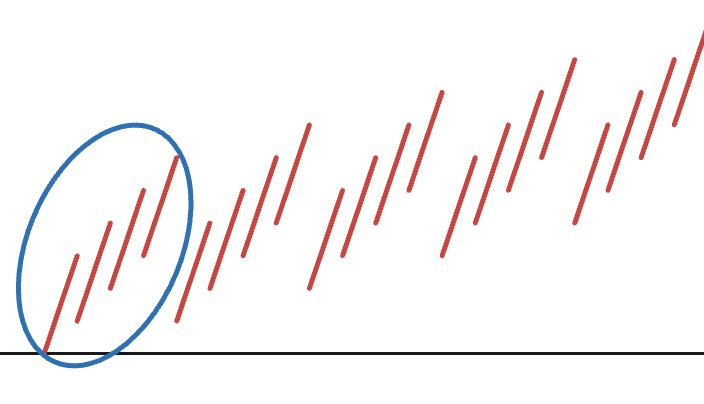
I wrote in more detail about my Do Nows here. One of this week’s Do Nows is below. The puzzle on the right is called a Shikaku puzzle from Naoki Inaba. For the first one, the goal is to divide the shape into three rectangles with sizes 3, 12, and 16. We rotate through different puzzles like these throughout the year, working on each puzzle type for a few weeks. It’s an optional challenge for students but a good way to challenge them and keep students who finish quickly busy.
I get these estimation challenges from Estimation 180. Similar to the puzzles above we rotate through different routines over the year, sticking with each routine for a few weeks. I wrote more about these types of routines here.
I’m on the record as being pretty skeptical of technology in math class. DeltaMath is the best tool I’ve found because it’s easy to give students mixed practice of multiple skills at once. Digital practice is also helpful because students are usually able to work more independently. I use that time to follow up individually with students who I know need some extra support. I also call these assignments “homework,” and parents really like hearing that there’s homework in my class. I’m really skeptical of the value of homework today because of how easy cheating has become. I give students lots of practice in class, and we start every assignment in class, so I know students are practicing. I don’t want to spend lots of time putting together and tracking down paper-and-pencil homework assignments if a significant number of students just punch it into PhotoMath or ChatGPT.
Pictured below is my mini-whiteboard setup at each table. Each table has calculators (only allowed for some parts of class), whiteboards, markers, and rags to erase with. It is unfortunately beyond my powers as a teacher to prevent students from drawing on the supply caddies. Mini whiteboards are a pain to manage sometimes but they are 100% worth it. There is no better way to quickly check student understanding.
One of the bread-and-butter things we do all the time in my math class is I give out a piece of paper with 8 or 12 or 16 problems (the exact number depends on how long the problems are), have students try them, and then figure out what to do next. I can have students check with a partner and then ask any questions they have. Or I can circulate, notice a problem students are stuck on, and do a quick re-teach. Or I can notice a common mistake and launch a discussion. Or I can realize it’s a mess and I need to do a bigger re-teach tomorrow. I often follow up with some quick mini whiteboard practice if there’s a common mistake I want to fix. These vary period to period. I realize this sounds boring and mundane but it only takes a few minutes, and these quick chunks of practice are the backbone of teaching multiple strands at once.
Desmos activities, now housed at Amplify, are the one digital tool I still use beyond DeltaMath. I used to do these all the time, and often spend most of the period on one activity. I’ve moved away from that as I’ve become more skeptical of computer-based learning. Now I’m much more likely to pick out a short chunk of a Desmos activity and use them as practice. Once the Chromebooks are out it is impossible to get every student’s attention without closing every Chromebook. The gravity of the screen is just too strong.
It can be tough to keep track of students struggling with what we’re learning given how many different things we do in a class. I keep a post-it on my desk, and during class I’ll jot down a few students who I see struggling with something. I do my best to follow up with them individually during DeltaMath work time at the end of class.
The prerequisite knowledge check is one of the most important things I do in class each day. If my lesson assumes students know something, I need to make sure they know it and re-teach it if they don’t. Mini whiteboards are by far the best way to do this.
I wrote more about my approach to fact fluency here. This operates like a parallel strand throughout the year. We’ve finished focused practice on 2s, 10s, 5s, 4s, 3s, and 11s. That’s almost all the multiplication facts! There are only 16 facts left we haven’t touched on at all. Those are also the heart of what students need to be successful. I don’t use 7x8 or 9x6 as examples when introducing something like solving equations or multiplying with negatives. That’s also why including 11s is so helpful — they’re easy to learn, so I use lots of 11s when we’re first learning something like multiplying negatives. Students can then focus their mental energy on the new thing — the negatives — and not trying to remember tricky multiplication facts.
Most weeks I do a quick presentation on a mathematician. It’s fun, I get to tell interesting stories about math, and students get to hear about all the different stuff mathematicians do. I interpret “mathematician” broadly — my list includes more famous mathematicians like Ramanujan and Emmy Noether but also lesser-known people like Gladys West, interesting stories like Chika Ofili, mathematical artists like Dylan Thomas, and contemporary people like Ayliean MacDonald. I try to get a broad range of identities to show students that mathematicians are diverse and come from all sorts of places. Desmos has a nice list if you want a place to start doing something like this.
There’s a tacit agreement in many math classrooms that the class learns a topic, they practice a bit, they take a quiz, they move on, and students mostly forget. That’s dumb. All of my quizzes mix in all three strands and topics from weeks or months before. This helps me know what I need to re-teach, and it also sends a message to students that all the spacing and retrieval practice is for a reason, and I expect them to remember what they’ve learned.
My district only has school four days a week. Long story, but the short version is that Colorado only requires 160 days of school each year. We have school four days a week each week and still have a weeklong Thanksgiving break, two weeks for winter break, a week for spring break, and seven weeks off over the summer.