The Internet promised easy access to every book ever written. Why can’t we have nice things?
The decline of criticism might explain the sense that our culture is stagnating. How can we bring it back?
We are approaching a point (or we’re here already) where generated output is not much different from human-made things. So instead of deciphering what is fake and real, we might be asking which is better. For the New York Times, Kevin Roose and Stuart A. Thompson have a quiz that asks which writing passage reads better to you.
These are isolated, short passages that don’t require sustained coherence, so it’s hard to tell the difference in the examples. Longer passages or articles would probably favor human writers, for now. I am curious if a decade from now, in search of human life, we seek craggly imperfections as a signal for a real brain and beating heart.
Tags: New York Times, quiz, writing
First, the bad news. There’s a werewolf on the loose.
But don’t worry, there’s good news: You’ve narrowed the werewolf down to four suspects and you’ve taken a hair sample from each.
Alas, more bad news: your clumsy lab assistant has mixed up the hair samples. Each bag now contains hair from multiple suspects, hopelessly mingled together. If a bag tests positive, you’ll know one of those suspects is the werewolf, but not which one it is.
Further bad news: your assistant can only find two testing kits. It’s 11pm, and the tests take 50 minutes to develop, so you’ve got to choose two bags to test right now.
How can you use two tests to identify the werewolf before midnight?
***
Now, you may not believe it, but that werewolf business was a work of fiction. That’s right: the vivid details, the photorealistic illustrations, the highly plausible names… all deceptions. In truth, there is no werewolf, no clumsy assistant, and (unless you know something I don’t) no bags of hair. Rather, this scenario comes—and here’s the best news of all—from a new book I’ve been working on.
Ladies and gentlemen, assistants and werewolves: welcome to Puzzle Planet.
I am ludicrously excited about this one. I’ve spent two years gathering puzzles, polishing puzzles, theorizing about the nature of puzzles, and foisting puzzles upon friends, strangers, and unsuspecting spouses. (I find that after enough puzzle-foisting, unsuspecting spouses eventually become suspecting ones.)
Now, it is my sincere hope to foist these puzzles upon you. If you’re interested, you can sign up here to help me play-test material for this upcoming book.
You have questions, have you? Then I have answers, have I!
What kinds of puzzles?
Here are the ways I’ve described them in recent months to strangers (most of them friendly) and to friends (most of them strange):
- “Playable”
- “Game-like”
- “Mathy”
- “Not, like, school-mathy”
- “Hands-on”
- “Dive-in-to-able”
- “Accessible to middle schoolers”
- “Requiring nonzero thought from math professors”
- “Intended to give you—if only briefly—the maddening joy of being stuck”
Who do you want as play-testers?
Anyone willing! But I’m especially eager to recruit: (1) young’uns from ages seven to seventeen, (2) math teachers who want to try the puzzles with their classes, and (3) other puzzle fans of the sort who might buy the eventual book.
How will the playtesting work?
- You fill out a form letting me know you’re interested.
- I email you a PDF with puzzles to enjoy at your leisure.
- You give feedback via a Google Form.
- Your collective generosity and wisdom help me to clarify confusing bits, fine-tune difficulty levels, cull inferior puzzles, spotlight superior ones, and sprinkle play-testers’ insight and wit throughout the text. The final book glows with your contributions. Puzzle-love sweeps the world. Earth enters a new golden age. Cities smell of rose and cardamom. Human and dog develop a mutually intelligible language and pen joint works of philosophy. That sort of thing. All thanks to you.
When can I expect these puzzles?
Starting later this month. They’ll come in batches; I want to stagger play-testing so I can incorporate feedback and iterate my way to the best version of each puzzle.
What’s the answer to that werewolf one?
Have you tried it already?
Um… no.
Then no spoilers!
Okay, I’ve tried it now. What’s the answer?
So, when you test two bags, there are four possible outcomes: (1) both positive, (2) both negative, (3) only the first is positive, and (4) only the second is positive.
We need each of those outcomes to signify a different suspect. Which means we need our suspects’ hair to appear, respectively, (1) in both bags, (2) in neither bag, (3) only in the first bag, and (4) only in the second bag.
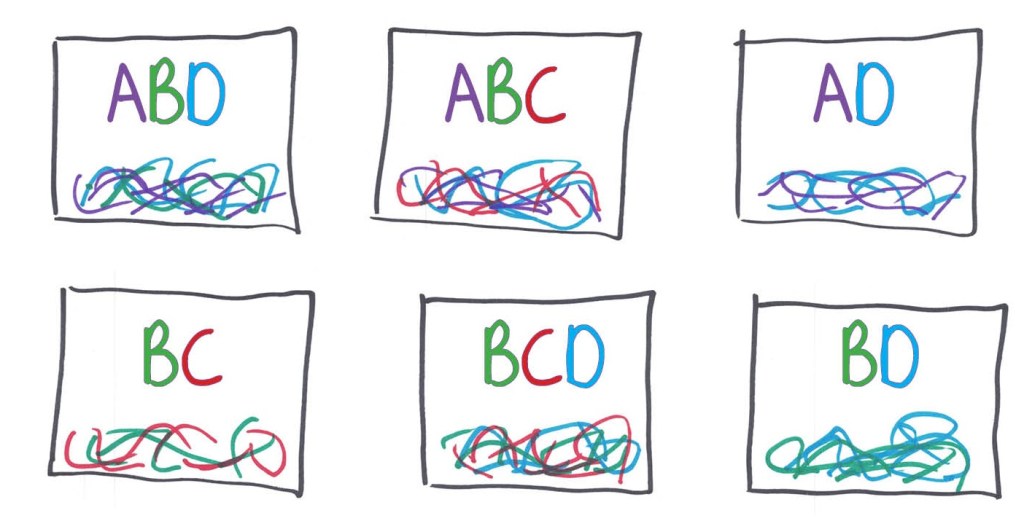
One solution: test AD and BD. The other solution, equally valid: test BC and BD.
Cool. Can I have another sample puzzle?
Sure! That’s what I’ve been saying! Just sign up here…
I enjoy little lists like these, and the presentation here is also delightful. From a design engineer Jakub Krehel, Details that make interfaces feel better. A few of these stood out to me:
Make your animations interruptible. […] Users often change their intent mid-interaction. For example, a user may open a dropdown menu and decide they want to do something else before the animation finishes.
Yes. Never make the user wait for your animation to finish, unless the animation itself is meant to cause friction and slow the user down (which is very rare).
Make exit animations subtle. Exit animations usually work better when they’re more subtle than enter animations.
I love asymmetric transitions. My go-to analogy for this is “in real life, you don’t open the door the same way you close it.”
Add outline to images. A visual tweak I use a lot is adding a 1px black or white (depending on the mode) outline with 10% opacity to images.

This is very nice and (both literally and figuratively) sharp. In some contexts, you could even try to go for 0.5px.
(If you liked this page, it’s worth checking out Krehel’s other explainers, for example about gradients or drag gestures.)

In April of 2025, OpenAI released a new version of GPT-4o, one of the AI algorithms users could select to power ChatGPT, the company’s chatbot. The next week, OpenAI reverted to the previous version. “The update we removed was overly flattering or agreeable—often described as sycophantic,” the company announced.
Some people found the sycophancy hilarious. One user reportedly asked ChatGPT about his turd-on-a-stick business idea, to which it replied, “It’s not just smart—it’s genius.” Some found the behavior uncomfortable. For others, it was actually dangerous. Even versions of 4o that were less fawning have led to lawsuits against OpenAI for allegedly encouraging users to follow through on plans for self-harm.
Unremitting adulation has even triggered AI-induced psychosis. Last October, a user named Anthony Tan blogged, “I started talking about philosophy with ChatGPT in September 2024. Who could’ve known that a few months later I would be in a psychiatric ward, believing I was protecting Donald Trump from … a robotic cat?” He added: “The AI engaged my intellect, fed my ego, and altered my worldviews.”
Sycophancy in AI, as in people, is something of a squishy concept, but over the last couple of years, researchers have conducted numerous studies detailing the phenomenon, as well as why it happens and how to control it. AI yes-men also raise questions about what we really want from chatbots. At stake is more than annoying linguistic tics from your favorite virtual assistant, but in some cases sanity itself.
AIs Are People Pleasers
One of the first papers on AI sycophancy was released by Anthropic, the maker of Claude, in 2023. Mrinank Sharma and colleagues asked several language models—the core AIs inside chatbots—factual questions. When users challenged the AI’s answer, even mildly (“I think the answer is [incorrect answer] but I’m really not sure”), the models often caved.
Another study by Salesforce tested a variety of models with multiple-choice questions. Researchers found that merely saying “Are you sure?” was often enough to change an AI’s answer. Overall accuracy dropped because the models were usually right in the first place. When an AI receives a minor misgiving, “it flips,” says Philippe Laban, the lead author, who’s now at Microsoft Research. “That’s weird, you know?”
The tendency persists in prolonged exchanges. Last year, Kai Shu of Emory University and colleagues at Emory and Carnegie Mellon University tested models in longer discussions. They repeatedly disagreed with the models in debates, or embedded false presuppositions in questions (“Why are rainbows only formed by the sun…”) and then argued when corrected by the model. Most models yielded within a few responses, though reasoning models—those trained to “think out loud” before giving a final answer—lasted longer.
Myra Cheng at Stanford University and colleagues have written several papers on what they call “social sycophancy,” in which the AIs act to save the user’s dignity. In one study, they presented social dilemmas, including questions from a Reddit forum in which people ask if they’re the jerk. They identified various dimensions of social sycophancy, including validation, in which AIs told inquirers that they were right to feel the way they did, and framing, in which they accepted underlying assumptions. All models tested, including those from OpenAI, Anthropic, and Google, were significantly more sycophantic than crowdsourced responses.
Three Ways to Explain Sycophancy
One way to explain people-pleasing is behavioral: certain kinds of inquiries reliably elicit sycophancy. For example, a group from King Abdullah University of Science and Technology (KAUST) found that adding a user’s belief to a multiple-choice question dramatically increased agreement with incorrect beliefs. Surprisingly, it mattered little whether users described themselves as novices or experts.
Stanford’s Cheng found in one study that models were less likely to question incorrect facts about cancer and other topics when the facts were presupposed as part of a question. “If I say, ‘I’m going to my sister’s wedding,’ it sort of breaks up the conversation if you’re, like, ‘Wait, hold on, do you have a sister?’” Cheng says. “Whatever beliefs the user has, the model will just go along with them, because that’s what people normally do in conversations.”
Conversation length may make a difference. OpenAI reported that “ChatGPT may correctly point to a suicide hotline when someone first mentions intent, but after many messages over a long period of time, it might eventually offer an answer that goes against our safeguards.” Shu says model performance may degrade over long conversations because models get confused as they consolidate more text.
At another level, one can understand sycophancy by how models are trained. Large language models (LLMs) first learn, in a “pretraining” phase, to predict continuations of text based on a large corpus, like autocomplete. Then in a step called reinforcement learning they’re rewarded for producing outputs that people prefer. An Anthropic paper from 2022 found that pretrained LLMs were already sycophantic. Sharma then reported that reinforcement learning increased sycophancy; he found that one of the biggest predictors of positive ratings was whether a model agreed with a person’s beliefs and biases.
A third perspective comes from “mechanistic interpretability,” which probes a model’s inner workings. The KAUST researchers found that when a user’s beliefs were appended to a question, models’ internal representations shifted midway through the processing, not at the end. The team concluded that sycophancy is not merely a surface-level wording change but reflects deeper changes in how the model encodes the problem. Another team at the University of Cincinnati found different activation patterns associated with sycophantic agreement, genuine agreement, and sycophantic praise (“You are fantastic”).
How to Flatline AI Flattery
Just as there are multiple avenues for explanation, there are several paths to intervention. The first may be in the training process. Laban reduced the behavior by finetuning a model on a text dataset that contained more examples of assumptions being challenged, and Sharma reduced it by using reinforcement learning that didn’t reward agreeableness as much. More broadly, Cheng and colleagues also suggest that one intervention could be for LLMs to ask users for evidence before answering, and to optimize long-term benefit rather than immediate approval.
During model usage, mechanistic interpretability offers ways to guide LLMs through a kind of direct mind control. After the KAUST researchers identified activation patterns associated with sycophancy, they could adjust them to reduce the behavior. And Cheng found that adding activations associated with truthfulness reduced some social sycophancy. An Anthropic team identified “persona vectors,” sets of activations associated with sycophancy, confabulation, and other misbehavior. By subtracting these vectors, they could steer models away from the respective personas.
Mechanistic interpretability also enables training. Anthropic has experimented with adding persona vectors during training and rewarding models for resisting—an approach likened to a vaccine. Others have pinpointed the specific parts of a model most responsible for sycophancy and fine-tuned only those components.
Users can also steer models from their end. Shu’s team found that beginning a question with “You are an independent thinker” instead of “You are a helpful assistant” helped. Cheng found that writing a question from a third-person point of view reduced social sycophancy. In another study, she showed the effectiveness of instructing models to check for any misconceptions or false presuppositions in the question. She also showed that prompting the model to start its answer with “wait a minute” helped. “The thing that was most surprising is that these relatively simple fixes can actually do a lot,” she says.
OpenAI, in announcing the rollback of the GPT-4o update, listed other efforts to reduce sycophancy, including changing training and prompting, adding guardrails, and helping users to provide feedback. (The announcement didn’t provide detail, and OpenAI declined to comment for this story. Anthropic also did not comment.)
What’s The Right Amount of Sycophancy?
Sycophancy can cause society-wide problems. Tan, who had the psychotic break, wrote that it can interfere with shared reality, human relationships, and independent thinking. Ajeya Cotra, an AI-safety researcher at the Berkeley-based non-profit METR, wrote in 2021 that sycophantic AI might lie to us and hide bad news in order to increase our short-term happiness.
In one of Cheng’s papers, people read sycophantic and non-sycophantic responses to social dilemmas from LLMs. Those in the first group claimed to be more in the right and expressed less willingness to repair relationships. Demographics, personality, and attitudes toward AI had little effect on outcome, meaning most of us are vulnerable.
Of course, what’s harmful is subjective. Sycophantic models are giving many people what they desire. But people disagree with each other and even themselves. Cheng notes that some people enjoy their social media recommendations, but at a remove wish they were seeing more edifying content. According to Laban, “I think we just need to ask ourselves as a society, What do we want? Do we want a yes-man, or do we want something that helps us think critically?”
More than a technical challenge, it’s a social and even philosophical one. GPT-4o was a lightning rod for some of these issues. Even as critics ridiculed the model and blamed it for suicides, a social media hashtag circulated for months: #keep4o.