a short about making art
starring kris mukai and arlin ortiz
In the early 1980s, if you wanted posters to advertise a yard sale or a party, your options were pretty limited.
You could get some blank sheets of paper and some crayons or felt markers for the whole do-it-yourself experience, which was cheap but unless you were a professional illustrator the results were bound to leave something to be desired, if not be downright embarrassing. Otherwise you could get the local printer to do it but it wasn’t going to be very cost-effective, especially in such a small quantity. Each poster could end up running you the same price as a Big Mac – or even a whole Meal Deal – and with that kind of overhead it could make the whole yard sale endeavour smell much less appetizing. And so, usually it was back to the felt markers or whatever else you could find lying around the house, and being the tightwad you were you would not-so-happily contribute an additional indignity to the ever-growing mountain of your own personal shame, because you wanted that Big Mac for yourself, dammit.

And let’s not even get started on greeting cards, those vile instruments of larceny that existed only to relieve you of your Big Mac money because if you didn’t buy them for every birthday, wedding, anniversary and holiday to give to every family member, friend, co-worker and all the other people you were even remotely acquainted with, you were certain to be outed as the tightwad you were and they might not want to be seen in public with you anymore. Which would leave you sitting in McDonald’s eating your Big Mac alone, plotting your revenge against Hallmark for engineering the single greatest extortion racket in the history of rackets. Curse you, Hallmark. Curse you!
But luckily for you, things weren’t going to remain this way forever. Home computer manufacturers began to get into some pretty serious price wars with each other, making their products much cheaper than they had been, and hence more accessible for tightwads like yourself. If you wanted to be really frugal, you could save your Big Mac money and convince your boss or parent to buy one! Totally win-win, right?

However, while the computer could theoretically handle the artistic part of things better than your own two thoroughly uncultured hands, there wasn’t yet e-mail or Facebook with which to send your digital creations, and there were no kiosks at Officeworks or Kinko’s where you could actually render your new digital servant’s creations to paper without having to pay that blasted printer all of your Big Mac money! You needed your own printing device (also co-incidentally called a printer) but you had to be patient because all you (or your parents or boss) could afford was a ‘daisy wheel’ model that punched out each character fully-formed like a typewriter, and unless you were proficient in ASCII art was quite useless for making posters and/or greeting cards, thus doing nothing to fill your stomach with more Big Macs. Curse you, Daisy!
But happily the printer manufacturers began to race for the bottom of the market (e.g. you) and soon dot-matrix models (which could print graphics) began to appear at a price more palatable to you (or whoever else you could talk into buying one). But then it turned out that designing the computer graphics yourself was tedious and time consuming, and you started longing for the felt markers and crayons. Now what?

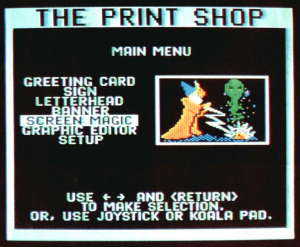
What you needed was software specifically designed to create posters and greeting cards without needing much effort on your part – a kind of… well, a computerised ‘print shop’ that wasn’t out to steal your Big Macs. Fortunately for you, a few enterprising individuals must have heard your pleas, because lo and behold, in 1984 software publisher Brøderbund released… well, ‘The Print Shop’, a program designed to create posters, greeting cards and other things without much effort on your part. If you had an Apple II that is. But you didn’t, because you were a tightwad who bought a Commodore 64 (or convinced someone else to) and so you had to wait an extra year before it came out for it (and the Atari 8-bit machines, also popular with tightwads after Jack Tramiel took Atari over and got into a price war with his former company). But you were happy to wait.
Because for around $50 (not your $50 of course, but your boss’s or your parents’ – or maybe you pirated it because why pay for software when you can buy Big Macs?) you could finally stick it to your local printer and Hallmark and all those other greedy bastards who picked your pocket and emptied your stomach. Hooray!

You could print out signs and posters for just about anything, as many as you liked. You could print our greeting cards for friends, family, everyone and anyone – even your dog, cat and goldfish (“Thank you for being such a lovely fish!”) You might even print out a greeting card congratulating you for your newfound ability to print out greeting cards! Why not? All it cost was a bit of ink and paper! But you weren’t the only one ecstatic for the prospect of this new innovation freeing you forever from the joint tyranny of Big Printing and Big Crayon. There were plenty of other people who needed to stretch a buck, and not just so they could stuff themselves with Big Macs. These included not-for-profit organisations who had previously done much of their in-house printing using wood blocks and ink pads (what is this, the 15th century?) and small businesses, which could now use the same computer and printer they bought for doing accounting to print flyers and posters.

Schools were also really big customers, The Print Shop being a saviour for time- and cash-poor teachers traditionally forced to rope students into drawing banners and posters – not always the easiest of tasks, and one that required some measure of supervision lest little Jimmy stick the felt markers up his nose. To sweeten the deal, Brøderbund came out with an additional ‘companion’ disk that could print customised calendars – what 1980s teacher wouldn’t want that? – and more fonts and graphics. It was an easy sale to make.

And boy did they sell! Sales took off like a rocket and developers Martin Kahn and David Balsam were rich overnight. The teenage whiz kid Brøderbund CEO Doug Carlston found to convert the program to work on other computers very quickly owned a Porsche! They no longer needed to worry about saving enough pocket change to buy a Big Mac (lucky bastards!) But The Print Shop did much more than simply enable its creators to purchase Porsches full of Big Macs – it proved there was a market for its sort of software.
With no self-interest at all, the publishing industry was extremely skeptical of the emerging threat posed to them by low-cost home computers and dot-matrix printers, mocking the ‘poor quality’ output they produced as unsuitable for anything anyone would dare show to anyone else – but The Print Shop demonstrated people’s standards were much lower than they had anticipated. All kidding aside, a new middle ground was established (somewhere between markers and markup) and other software publishers eagerly jumped into it, creating not just ripoffs like PrintMaster, but new software such as The Newsroom, Create-A-Calendar and Awardware, each designed to provide a new ‘good enough’ solution in an area previously limited to professional or handmade alternatives.

These applications formed the foundation upon which the desktop publishing industry was built –sure, the Macintosh and LaserWriter invaded the commercial printing industry, but they would have had a harder time had software like The Print Shop not aided in fostering an acceptance of computer-generated print media by the general public first. And the demand for consumer self-publishing solutions didn’t end there – lower cost 16-bit computers such as the Atari ST combined with cheaper design packages such as Timeworks Desktop Publisher and higher-quality 24-pin printers meant that those computer users who had previously found such great utility in The Print Shop and its brethren were able to advance in their amateur printing wizardry to full-scale in-the-box design, creating everything from brochures to how-to books in the comfort of their own homes – and without sacrificing too many Big Macs.

This trend would continue to the present day where obtaining the tools needed to create a publication such as this magazine are within the reach of most. But sadly, while the future was made of happy fonts and clip-art celebrations for many, for some – including Brøderbund’s founders and many of its employees – it would not go so well. After a competitor to The Print Shop called PrintMaster appeared, Brøderbund sued – and won, but this story does not end there, with PrintMaster’s publisher Mindscape making the required changes to avoid legal reprecussions and continuing to market it. But venture capitalist-backed SoftKey, looking to ‘consolidate’ the software industry, saw an opportunity to weaken Brøderbund, buying Mindscape and virtually giving away PrintMaster, hurting Brøderbund’s profits and lowering its stock price. SoftKey mounted a hostile takeover and 500 employees lost their jobs. Bummer!

Cognitive load is what matters
Excellent living document (the underlying repo has 625 commits since being created in May 2023) maintained by Artem Zakirullin about minimizing the cognitive load needed to understand and maintain software.This all rings very true to me. I judge the quality of a piece of code by how easy it is to change, and anything that causes me to take on more cognitive load - unraveling a class hierarchy, reading though dozens of tiny methods - reduces the quality of the code by that metric.
Lots of accumulated snippets of wisdom in this one.
Mantras like "methods should be shorter than 15 lines of code" or "classes should be small" turned out to be somewhat wrong.
Via @karpathy
Tags: programming, software-engineering
This is not at all news, but it comes up often enough that I think there should be a concise explanation of the problem. People, myself included, like to say that POSIX time, also known as Unix time, is the number of seconds since the Unix epoch, which was 1970-01-01 at 00:00:00.
This is not true. Or rather, it isn’t true in the sense most people think. For example, it is presently 2024-12-25 at 18:54:53 UTC. The POSIX time is 1735152686. It has been 1735152715 seconds since the POSIX epoch. The POSIX time number is twenty-nine seconds lower.
This is because POSIX time is derived in IEEE 1003.1 from Coordinated Universal Time. The standard assumes that every day is exactly 86,400 seconds long. Specifically:
The time() function returns the value of time in seconds since the Epoch.
Which is defined as:
seconds since the Epoch. A value to be interpreted as the number of seconds between a specified time and the Epoch. A Coordinated Universal Time name (specified in terms of seconds (tm_sec), minutes (tm_min), hours (tm_hour), days since January 1 of the year (tm_yday), and calendar year minus 1900 (tm_year)) is related to a time represented as seconds since the Epoch according to the expression below.
If year < 1970 or the value is negative, the relationship is undefined. If year ≥ 1970 and the value is non-negative, the value is related to a Coordinated Universal Time name according to the expression:
tm_sec + tm_min * 60 + tm_hour * 3600 + tm_yday * 86400 + (tm_year-70) * 31536000 + ((tm_year - 69) / 4) * 86400
The length of the day is not 86,400 seconds, and in fact changes over time. To keep UTC days from drifting too far from solar days, astronomers periodically declare a leap second in UTC. Consequently, every few years POSIX time jumps backwards, wreaking utter havoc. Someday it might jump forward.
Archaeology
Appendix B of IEEE 1003 has a fascinating discussion of leap seconds:
The concept of leap seconds is added for precision; at the time this standard was published, 14 leap seconds had been added since January 1, 1970. These 14 seconds are ignored to provide an easy and compatible method of computing time differences.
I, too, love to ignore things to make my life easy. The standard authors knew “seconds since the epoch” were not, in fact, seconds since the epoch. And they admit as much:
Most systems’ notion of “time” is that of a continuously-increasing value, so this value should increase even during leap seconds. However, not only do most systems not keep track of leap seconds, but most systems are probably not synchronized to any standard time reference. Therefore, it is inappropriate to require that a time represented as seconds since the Epoch precisely represent the number of seconds between the referenced time and the Epoch.
It is sufficient to require that applications be allowed to treat this time as if it represented the number of seconds between the referenced time and the Epoch. It is the responsibility of the vendor of the system, and the administrator of the system, to ensure that this value represents the number of seconds between the referenced time and the Epoch as closely as necessary for the application being run on that system….
I imagine there was some debate over this point. The appendix punts, saying that vendors and administrators must make time align “as closely as necessary”, and that “this value should increase even during leap seconds”. The latter is achievable, but the former is arguably impossible: the standard requires POSIX clocks be twenty-nine seconds off.
Consistent interpretation of seconds since the Epoch can be critical to certain types of distributed applications that rely on such timestamps to synchronize events. The accrual of leap seconds in a time standard is not predictable. The number of leap seconds since the Epoch will likely increase. The standard is more concerned about the synchronization of time between applications of astronomically short duration and the Working Group expects these concerns to become more critical in the future.
In a sense, the opposite happened. Time synchronization is always off, so systems generally function (however incorrectly) when times drift a bit. But leap seconds are rare, and the linearity evoked by the phrase “seconds since the epoch” is so deeply baked in to our intuition, that software can accrue serious, unnoticed bugs. Until a few years later, one of those tiny little leap seconds takes down a big chunk of the internet.
What To Do Instead
If you just need to compute the duration between two events on one computer, use CLOCK_MONOTONIC. If you don’t need to exchange timestamps with other systems that assume POSIX time, use TAI, GPS, or maybe LORAN. If you do need rough alignment with other POSIX-timestamp systems, smear leap seconds over a longer window of time. Libraries like qntm’s t-a-i can convert back and forth between POSIX and TAI.
There’s an ongoing effort to end leap seconds, hopefully by 2035. It’ll require additional work to build conversion tables into everything that relies on the “86,400 seconds per day” assumption, but it should also make it much simpler to ask questions like “how many seconds between these two times”. At least for times after 2035!
We keep trying to get LLMs to do math. We want them to count the number of “rs” in strawberry, to perform algebraic reasoning, do multiplication, and to solve math theorems.
A recent experiment particularly piqued my interest. Researchers used OpenAI’s new 4o model to solve multiplication problems by using the prompt:
Calculate the product of x and y. Please provide the final answer in the format:
Final Answer: [result]
These models are generally trained for natural language tasks, particularly text completions and chat.
So why are we trying to get these enormous models, good for natural text completion tasks like summarization, translation, and writing poems, to multiply three-digit numbers and, what’s more, attempt to return the results as a number?
Two reasons:
- Humans always try to use any new software/hardware we invent to do calculation
- We don’t actually want them to do math for the sake of replacing calculators, we want to understand if they can reason their way to AGI.
Computers and counting in history
In the history of human relationships with computers, we’ve always wanted to count large groups of things because we’re terrible at it. Initially we used our hands - or others’ - in the Roman empire, administrators known as calculatores and slaves known as calculones performed household accounting manually.
Then, we started inventing calculation lookup tables. After the French Revolution, the French Republican government switched to the metric system in order to collect property taxes. In order to perform these calculations, it hired human computers to do the conversions by creating large tables of logarithms for decimal division of angles, Tables du Cadastre. This system was never completed and eventually scrapped, but it inspired Charles Babbage to do his work on machiens for calculation along with Ada Lovelace, which in turn kicked off the modern era of computing.
UNIVAC, one of the first modern computers, was used by the Census Bureau in population counting.
The nascent field of artificial intelligence developed jointly in line with the expectation that machines should be able to replace humans in computation through historical developments like the Turing Test and Turing’s chess program, the Dartmouth Artificial Intelligence Conference and Arthur Samuel’s checkers demo.
Humans have been inventing machines to mostly do math for milennia, and it’s only recently that computing tasks have moved up the stack from calculations to higher human endeavors like writing, searching for information, and shitposting. So naturally, we want to use LLMs to do the thing we’ve been doing with computers and software all these years.
Making computers think
Second, we want to understand if LLMs can “think.” There is no one definition of what “thinking” means, but for these models in particular, we are interested to see if they can work through a chain of steps to come to an answer about logical things that are easy for humans, as an example:
all whales are mammals, all mammals have kidneys; therefore, all whales have kidneys
One way humans reason is through performing different kinds of math: arithmetic, solving proofs, and reasoning through symbolic logic. The underlying question in artificial intelligence is whether machines can reason outside of the original task we gave them. For large language models, the ask is whether they can move from summarizing first a book if they were trained for books, to a movie script plot, to finally, summarizing what you did all day if you pass it a bunch of documents about your activity. So, it stands to reason that if LLMs can “solve” math problems, they can achieve AGI.
There are approximately seven hundred million benchmarks to see if LLMs can reason. Here’s an example, and here’s another one. Even since I started this draft yesterday, a new one came out.
Since it’s hard to define what “reasoning” or “thinking” means, the benchmarks try to proxy to see if models can answer the same questions we give to humans in settings such as university tests and compare the answers between human annotators generating ground truth and inference run on the model.
These types of tasks make up a large number of LLM benchmarks that are popular on LLM leaderboards.
How calculators work
However, evaluating how good LLMs are at calculation doesn’t take into account a critical component: the way that calculators arrive at their answer is radically different from how these models work. A calculator records the button you pressed and converts it to a binary representation of those digits. Then, it stores those number in memory registers until you press an operation key. For basic hardware calculators, the machine has built-in operations that perform variations of addition on the binary representation of the number stored in-memory:
+ addition is addition,
+ subtraction is performed via two's complement operations,
+ multiplication is just addition, and
+ division is subtraction
In software calculators, the software takes user keyboard input, generates a scan code for that key press, encodes the signal, converts it to character data, and uses an encoding standard to convert the key press to a binary representation. That binary representation is sent to the application level, which now starts to work with the variable in the programming language the calculator uses, and performs operations on those variables based on internally-defined methods for addition, subtraction, multiplication, and division.
Software calculators can grow to be fairly complicated with the addition of graphing operations and calculus, but usually have a standard collected set of methods to follow to perform the actual calcuation. As a fun aside, here’s a great piece on what it was like to build a calculator app Back In The Day.
The hardest part of the calculator is writing the logic for representing numbers correctly and creating manual classes of operations that cover all of math’s weird corner cases.
However, to get an LLM to add “2+2”, we have a much more complex level of operations. Instead of a binary calculation machine that uses small, simple math business logic to derive an answer based on addition, we create an enormous model of the entire universe of human public thought and try to reason our way into the correct mathematical answer based on how many times the model has “seen” or been exposed to the text “2+2” in written form.
We first train a large language model to answer questions.
This includes:
- Gathering and deduplicating an enormous amount of large-scale, clean internet text
- We then train the model by feeding it the data and asking it, at a very simplified level, to predict the next word in a given sentence. We then compare that prediction to the baseline sentence and adjust a loss function. An attention mechanism helps guide the prediction by keeping a context map of all the words of our vocabulary (our large-scale clean internet text.)
- Once the model is trained initially to perform the task of text completion, we perform instruction fine-tuning, to more closely align the model with the task of performing a summarization task or following instructions.
- The model is aligned with human preferences with RLHF. This process involves collecting a set of questions with human responses, and having human annotators rank the response of the model, and then feeding those ranks back into the model for tuning.
- Finally, we stand up that artifact (or have it accessable as a service.) The artifact is a file or a collection of files that contain the model architecture and weights and biases of the model generated from steps 2 and 3.
Then, when we’re ready to query our model. This is the step that most people take to get an answer from an LLM when they hit a service or run a local model, equivalent to opening up the calculator app.
- We write “What’s 2 + 2” into the text box.
- This natural-language query is tokenized. Tokenization is the process of first converting our query into a string of words that the model uses as the first step in performing numerical lookups.
- That text is then embedded in the context of the model’s vocabulary by converting each word to an embedding and then creating an embedding vector of the input query.
- We then passing the vector to the model’s encoder, which stores the relative position of embeddings to each other in the model’s vocabulary
- Passing those results to the attention mechanism for lookup, which compares the similarity using various metrics of each token and position with every other token in the reference text (the model). This happens many times in multi-head attention architectures.
- Getting results back from the decoder. A set of tokens and the probability of those tokens is returned from the decoder. We need to generate the first token that all the other tokens are conditioned upon. However, afterwards, returning probablities takes many forms: namely search strategies like greedy search and and sampling, most frequently top-k sampling, the method originally used by GPT-2. Depending on which strategy you pick and what tradeoffs you’d like to make, you will get slightly different answers of resulting tokens selected from the model’s vocabulary.
Finally, even after this part, to ensure that what the model outputs is an actual number, we could do a number of different guided generation strategies to ensure we get ints or longs as output from multiplication, addition, etc.
So this entire process, in order to add “what is 2+2”, we do a non-deterministic a lookup from an enormous hashtable that contains the sum of public human knowledge we’ve seen fit to collect for our dataset, then we squeeze it through the tiny, nondeterministic funnels of decoding strategies and guided generation to get to an answer from a sampled probability distribution.
These steps include a large amount of actual humans in the loop guiding the model throughout its various stages.
And, all of this, only to get an answer that’s right only some percent of the time, not consistent across all model architectures and platforms and in many cases has to be coaxed out of the model using techniques like chain of thought.
As an example, here’s an aswer I’ve tried on OpenAI, Claude, Gemini, and locally using Mistral via llamafile and ollama:
If you ask any given calculator what 2+2 is, you’ll always get 4. This doesn’t work with LLMs, even when it’s variations of the same model, much less different models hosted across different service providers and in different levels of quantization, different sampling strategies, mix of input data, and more.
Why are we even doing this?
From a user perspective, this is absolutely a disastrous violation of Jakob’s Law of UX, which states that people expect the same kind of output from the same kind of interface.
However, when you realize that the goal is, as Terrence Tao notes, to get models to solve mathematical theorems, it makes more sense, although all these models are still very far from actual reasoning.
I’d love to see us spend time more understanding and working on the practical uses he discusses: drafts of documents, as ways to check understanding of a codebase, and of course, generating boilerplate Pydantic models for me personally.
But, this is the core tradeoff between practicality and research: do we spend time on Pydantic now because it’s what’s useful to us at the moment, or do we try to get the model to write the code itself to the point where we don’t even need Pydantic, or Python, or programming languages, and can write natural language code, backed by mathematical reasoning?
If we didn’t spend time on the second, we never would have gotten even to GPT-2, but the question is, how much further can we get? I’m not sure, but I personally am still not using LLMs for tasks that can’t be verified or for reasoning, or for counting Rs.
Further Reading: